Bohrov model atoma
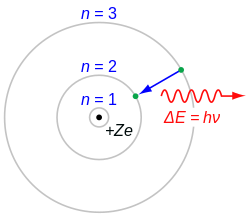




Bohrov model atoma je dopuna Rutherfordovog modela atoma s dva postulata i time je uspio objasniti strukturu elektronskog omotača i procese emisije i apsorpcije svjetlosti. Ideju kvantizacije, koju su M. Planck i A. Einstein uveli za elektromagnetsko zračenje (foton), N. Bohr je primijenio na Rutherfordov planetni model vodikova atoma i objašnjavajući izmjerene valne duljine u spektru atomskoga vodika izveo načelo korespondencije koje povezuje klasičnu fiziku i kvantnu fiziku. U tu svrhu postavio je hipotezu da se elektron može gibati oko atomske jezgre samo po onim kružnim putanjama za koje je kutna količina gibanja cjelobrojni višekratnik veličine h/2π, gdje je h Planckova konstanta.[1] Na taj način dobio je fizikalnu sliku atoma koja se naziva Bohrov model atoma. U tom modelu elektron se može gibati oko jezgre samo po kružnim putanjama određenih polumjera: r1 = a, r2 = 4 a, r3 = 9 a, i tako dalje, ili općenito po putanjama polumjera rn = n2a, gdje je a = 0,53 · 10–10 m (Bohrov radijus) i n je cijeli broj. Energija vodikova atoma u stanju s polumjerom rn = n2a iznosi En = –13,6 eV.[1]
Vodikov atom emitira kvant elektromagnetskog zračenja (foton), kada elektron prelazi s neke više, n-te Bohrove putanje energije En, na neku nižu m-tu energije Em, i pritom emitira foton energije:
Iako se poslije pokazalo da Bohrov model može objasniti samo spektar vodikova atoma, imao je golemu važnost u razvoju fizike kao prvi pokušaj da se ideja o kvantizaciji primijeni na atome.[1]
Prvi Bohrov postulat[uredi | uredi kôd]
Elektron ne može kružiti oko jezgre po bilo kojim stazama, već samo po onima s točno određenim kvantiziranim stanjima. To su takozvane dopuštene ili stacionarne staze; gibajući se po njima elektron se nalazi u stacionarnom stanju, ne gubi energiju zračenjem elektromagnetskih valova. Dopuštene su samo one staze na kojim je orbitalni moment količine gibanja cjelobrojni višekratnik reducirane Planckove konstante, , odnosno, Bohr je izrazom , gdje je reducirana Planckova konstanta ili , kvantizirao gibanje elektrona u atomu. Prirodni broj n=1,2,3... se naziva i glavni kvantni broj.
Ako sada zaključimo da je centripetalna sila , gdje je m masa, v brzina a r radijus, koja se javlja pri kruženju elektrona u atomu, zapravo ništa drugo nego Coulombova sila , gdje je e naboj elektrona, a r polumjer, slijedi izvod za polumjer kružne putanje:
a jer je količina gibanja jednaka , slijed da je:
Ako lijevu i desnu strane jednadžbe pomnožimo sa imamo:
Prema kvantnom uvjetu, na desnu stranu jednadžbe umjesto uvrstimo jer je , a reducirana konstanta :
Iz te jednadžbe izvučimo polumjer:
gdje je n kvantni broj koji može poprimiti vrijednosti n=1,2,3, ... Bohr je ovu jednadžbu skratio uvevši oznaku a, , koja označava najmanji mogući polumjer kružne putanje; tako da se jednadžba može zapisati i kao . Vidimo da su vrijednosti koje sačinjavaju a konstante, pa je samim tim i a konstanta i iznosi a=0,53*10-10 metara i naziva se Bohrovim polumjerom.
Drugi Bohrov postulat[uredi | uredi kôd]
Atom apsorbira (upije) zračenje samo kada primi određeni kvant energije i emitira određeni kvant energije kada prelazi iz jednog stacionarnog stanja u drugo (to jest kada prelazi iz stanja više energije u stanje niže). Atom ne može sponatno preći iz stanja niže u stanje više energije, nego tek kada biva pogođen s određenim kvantom energije (fotonom). Prelazak iz višeg stanja u niže je spontan događaj, uokviren statističkom prirodom, pri čemu se emitira kvant energija (foton). Frekvencija emitiranog fotona pri spontanom prelasku iz višeg u niže energetsko stanje dana je jednadžbom:
gdje je energija fotona i , a je frekvencija fotona. Dakle, apsorpcijom fotona dolazi do eksitacije atoma - prelaska atoma iz niže u više energetsko stanje, a spontanom emisijom fotona dolazi do prijelaza atoma iz višeg u niže energetsko stanje.
Zaključak[uredi | uredi kôd]
Bohr se u svojim postulatima poslužio Planckovom teorijom o kvantu energije. Važno je uočiti da je Bohr potvrdio Einsteinovu formulaciju elektromagnetske svjetlosti kao roja fotona ili kvantna energije. Zbog toga što je uveo stacionarne staze, Bohr je oslobodio planetarnog modela atoma (model atoma koji prikazuje atom kao sustav "Sunce-planeti" u kojem elektroni kruže oko jezgre) starog problema iz klasične elektrodinamike koji je upućivao na to da bi elektron morao emitirati kontuniurani spektar elektromagnetskih valova i time gubiti energiju dok se napokon ne bi urušio u jezgru. Još jedan dokaz u prilog stacionarnih staza su linijski spektri atoma, od kojih je najpoznatija Pascheonova, Balmerova i Lymanova serija vodikova spektra, koje je Bohr riješio svojim postulatima.
Bohrov model nuklearnih procesa[uredi | uredi kôd]
Godine 1935. postavio je N. Bohr razvidan model pretvorbi atomskih jezgri, koji dobro tumači opažane reakcije. Po Bohru u pretvorbama atomskih jezgri možemo pronaći 3 koraka: 1. čestica koja ulazi kao projektil ulazi u atomsku jezgru. Zbog kratkog dometa nuklearnih sila, projektil ima uzajamno djelovanje samo s nekoliko sastavnih čestica jezgre. On se "sudara" s njima, prenosi na njih svoju kinetičku energiju. Ove čestice dalje uzajamno djeluju s drugim česticama. Poslije nekog vremena energija projektila jednoliko se raspodjeljuje po čitavoj jezgri. S druge strane, projektil je izgubio toliko energije da više ne može umaći iz jezgre. On ostaje u jezgri. Ako je projektil spori neutron, on biva pri ulazu u jezgru snažno ubrzan od nuklearnih sila. Energija spajanja neutrona iznosi oko 8 MeV. Tolika energija je jezgri privedena kad ona uhvati spori neutron. 2. time što projektil ostaje u jezgri nastaje složena atomska jezgra koja traje relativno dugo vrijeme. Dugo vrijeme znači tu dugo prema vremenu što bi projektilu trebalo da projuri kroz jezgru. Složenu jezgru koja se nalazi u energetski višem, pobuđenom stanju možemo promatrati kao toplinski sustav. Privedena energija raspodjeljuje se na čestice po poznatom statističkom zakonu. Ako energija pobuđenja iznosi oko oko 10 MeV, tad temperatura jezgre iznosi 1010 apsolutnih stupnjeva. No, prema statističkom zakonu kolebanja, poslije izvjesnog vremena energija pobuđenja opet će se velikim dijelom koncentrirati na jednoj čestici. Time ovo međustanje prestaje. 3. čestica koja je skupila dovoljno energije otrgne se od jezgre. Atomska jezgra je izvršila pretvorbu. Očito je da je ovaj posljednji čin nezavisan od toga na koji je način proizvedena složena jezgra. Oba događaja da projektil pogodi jezgru i da se složena međujezgra raspadne nezavisni su jedan od drugog. Prema tome je i vjerojatnost neke pretvorbe produkt vjerojatnosti stvaranja i raspadanja složene međujezgre.
Jedan poznati primjer pokazat će nam na koliko različitih načina može biti stvorena međujezgra:
Bez obzira na to kako je nastala, složena jezgra može se dalje raspasti:
Vjerojatnost tog procesa zavisi smo od složene međujezgre. Vjerojatnost pretvorbe atomske jezgre umnožak je, dakle, dviju vjerojatnosti, vjerojatnost tvorbe i vjerojatnosti raspada složene jezgre.
Bohrov model pokazuje kako se na osnovu vrlo jednostavnih i općih predodžbi može postići razumijevanje vrlo složenih procesa kod pretvorbi atomskih jezgri. Ujedno vidimo kako su dalekosežni osnovni klasični zakoni u fizičkim procesima.[2]
Izvori[uredi | uredi kôd]
- ↑ a b c Bohr, Niels. Hrvatska enciklopedija. Leksikografski zavod Miroslav Krleža. 2015.
- ↑ Ivan Supek: "Nova fizika", Školska knjiga Zagreb, 1966.





























