Heisenbergovo načelo neodređenosti



Heisenbergovo načelo neodređenosti ili Heisenbergove relacije neodređenosti su bilo koja inačica nejednakosti koja govori o fundamentalnom ograničenju spoznaje vrijednosti komplementarnih fizikalnih veličina. Prvo takvo načelo uveo je 1927. njemački fizičar Werner Heisenberg, a formuliran je za fizikalne veličine položaja i količine gibanja: što točnije poznajemo položaj, manje točno možemo poznavati količinu gibanja - i obrnuto.[1] Heisenberg je izvorno svoje relacije izrazio preko matrične mehanike (koju je osmislio kao dvadesetdvogodišnjak, za potrebe kvantne mehanike, 1925. kada se povukao na otok Helgoland da bi izbjegao jake alergijske napade od kojih je patio[2]), to jest preko komutacijskih relacija:
gdje su: i operatori položaja i količine gibanja, a reducirana Planckova konstanta.
Kada se nejednakost izrazi preko standardne devijacije, kao što su to napravili E. H. Kennard i H. Weyl, postaje jasnije da je riječ o organičavanju znanja o položaju x i količini gibanja p:
gdje su: i standardne devijacije položaja i količine gibanja, definirane kao: i
U kvantnoj se teoriji, u literaturi, uobičajeno navode tri relacije za položaj i količinu gibanja:
te četvrta relacija neodređenosti za energiju i vrijeme:
Prema Heisenbergovim relacijama neodređenosti, nemoguće je oboje, položaj i količinu gibanja (na primjer elektrona), odrediti apsolutno točno, čak ni idealnim hipotetičkim pokusom, jer se postupkom mjerenja položaja nužno remeti količina gibanja, i obratno. Prema Heisenbergovim riječima, ne postoji, primjerice, stvarna staza elektrona u komori s mjehurićima, jer je svakim mjehurićem određen "ne posve točno" položaj, a brzina se elektrona određuje iz slijeda mjehurića. Heisenbergovo je stajalište do kraja jasno: elektron postoji neovisno o opažaču, ali se promatranjem na nj utječe onako kako je to formulirano matematičkom shemom relacija neodređenosti. Niti jedan do sada izveden pokus kojim ih se htjelo narušiti ili opovrgnuti nije uspio izbjeći relacije neodređenosti.[3]
Formulacije[uredi | uredi kôd]
Valno-mehanička formulacija[uredi | uredi kôd]
(Ref[4])
Prema de Broglievoj hipotezi, svaka čestica ima ujedno i valna svojstva. Informacije o položaju čestice, u kvantnoj mehanici, dobiva se iz valne funkcije . Vremenski neovisna valna funkcija za jednostavni ravni valnog broja k0 i količine gibanjap0 je
Vjerojatnost nalaženja čestice između a i b je, po Bornovom pravilu, definirana kao
Očito je da je u slučaju ravnoga valna funkcija konstanta, odnosno, čestica može biti bilo gdje, u promatranom prostoru, s jednakom vjerojatnosti. Drugim riječima, položaj čestice je maksimalno neodređen. Ako promatramo valnu funkciju koja je superpozicija više valova (kao na animaciji desno):
gdje A n predstavlja koeficijent, odnosno doprinos vala količine gibanja pn rezultantnom valu. Prijeđemo li sa sume po diskretnim valovima na kontinuirani slučaj, rezultantna valna funkcija bit će integral preko svih mogućih valova
gdje predstavlja amplitudu koja je Fourierov transform od . S ovom funkcijom, pozicija je postala preciznije definirana, ali je sada količina gibanja slabije definirana pošto je rezultantni val superpozicija valova s raznim količinama gibanja. Točnije, smanjili smo standardnu devijaciju pozicije σx na račun povećavanja standardne devijacije količine gibanja σp.
Stoga, ako povećamo σx, smanjit će se σp i obrnuto. Zaključujemo da je odnos σx i σp obrnuto proporcionalan, što je upravo ono što govore Heisenbergove relacije neodređenosti. Može se pokazati da umnožak σx i σp daje upravo vrijednost .
Matrična formulacija[uredi | uredi kôd]
(Ref[4])
U matričnoj mehanici, izvornom načinu na kojem je Heisenberg došao do svojih relacija, opservable poput položaja i količine gibanja samoadjungirani operatori. Za početak, definirajmo komutacijske relacije između dva operatora kao
U slučaju operatora položaja i količine gibanja, imamo
Neka je vlastita funkcija operatora položaja s konstantnom vlastitom vrijednosti x0, što per definitionem znači da je . Primijenimo spomenuti komutator na i dobit ćemo:
gdje je Î operator identiteta.
Pretpostavimo, radi reductio ad absurdum, da je ujedno i vlastita funkcija operatora količine gibanja, s vlastitom vrijednosti p0; tada bismo imali
Međutim, takav rezultat je upravo u kontradikciji s Heisenbergovim relacijama neodređenosti koje zahtijevaju
Što implicira da kvantna stanja ne mogu biti istovremeno vlastita funkcija položaja i količine gibanja. Drugim riječima: mjerenjem položaja, količina gibanja će biti neodređena, i obrnuto.
Važne relacije neodređenosti[uredi | uredi kôd]
Osim spomenutih relacija neodređenosti između položaja i količine gibanja, u kvantnoj mehanici često se koriste i relacije neodređenosti za: komponente kutne količine gibanja, komponente spina čestice i relacije između energije i vremena.
Za kutnu količinu gibanja vrijedi
Gdje je Levi-Civita simbol. Što znači da nije moguće istovremeno poznavati vrijednosti dviju komponenta kutne količine gibanja.
Za komponente spina vrijedne analogne relacije kao kod kutne količine gibanja, odnosno
Što znači da nije moguće istovremeno poznavati vrijednosti dviju komponenta spina.
Pošto vrijeme u nerelativističkoj kvantnoj mehanici nije opservabla, umjesto vremena koristi se životni vijek stanja u odnosu na opservablu B, pa relacije imaju oblik
gdje je σE standardna devijacija Hamiltonijana (operatora energije) u stanju , a σB standardna devijacija nekog operatora B.,[5] gdje je
Heisenbergov mikroskop[uredi | uredi kôd]
Relacije neodređenosti izmeđ položaj i brzinu neke čestice možemo predočiti slikovitim teorijskim primjerom Heisenbergova mikroskopa:

Da bismo promatranjem odredili položaj nekog tijela, moramo ga osvijetliti i primiti svjetlost koja se od njega reflektira. Međutim, zbog ogiba svjetlosti položaj tijela možemo odrediti najpreciznije na valnu duljinu svjetlosti pa tako možemo pisati da je neodređenost položaja tijela jednaka valnoj duljini svjetlosti (Δx≈λ). Smanjenjem valne duljine korištene svjetlosti možemo sve preciznije odrediti položaj tražene čestice, ali u tom slučaju povećavamo energiju zračenja (E=hf=hc/λ), odnosno čestična svojstva svjetlosti (elektromagnetskog vala) čiji foton u tom slučaju ima veću količinu gibanja (p=h/λ) pa tako u "sudaru" s promatranom česticom više mijenja njenu količinu gibanja (u odnosu na početnu) tako da je i nju nemoguće sasvim točno odrediti. Povećanjem čestičnih svojstava svjetlosti kojom osvjetljavamo (smanjenje valne duljine) gubi se na preciznosti mjerenja brzine (količine gibanja), a povećanjem valnih (povećanje valne duljine) gubi se na preciznosti određivanja položaja.
Ovo nije posljedica nesavršenosti mjernih instrumenata, nego je kvantno svojstvo samog promatranog sustava i nemoguće ga je izbjeći i uporabom savršenih mjernih instrumenata. Što preciznije mjerimo položaj, manje precizno mjerimo brzinu i obrnuto. Ovo svojstvo otkrio je 1927. godine njemački fizičar Werner Heisenberg a obično se formulira ovako:
Δp·Δx≥ħ/2
gdje je Δp neodređenost količine gibanja, Δx neodređenost položaja, a ħ je reducirana Planckova konstanta (ħ=h/2π) h=6,626·10−34 Js
ili drukčije formulirano:
ΔE·Δt≥ħ/2
gdje je ΔE neodređenost energije, a Δt neodređenost mjerenja vremenskog intervala.
Ove relacije vrijede i u makrosvijetu (svijetu klasične mehanike), ali tamo su neprimjetljive jer je neodređenost položaja zanemariva u odnosu na dimenzije tijela, a neodređenost količine gibanja u odnosu na ukupnu količinu gibanja tijela.
Heisenbergovo načelo neodređenosti izazvalo je brojne kritike u svijetu fizike 20. stoljeća (najpoznatije od Alberta Einsteina) jer je utjelovljenje kontrarnosti determinističkim principima dotadašnje fizike, otpočelo je eru probabilističkog pristupa kvantnoj fizici i postavilo bitnu granicu preciznosti eksperimenta.
Primjeri[uredi | uredi kôd]
Čestica u kutiji[uredi | uredi kôd]

Najjednostavniji kvantnomehanički sustav je primjer slobodne čestice u kutiji. Takva čestica se može gibati samo u jednoj dimenziji (lijevo-desno) i ograničena je u beskonačoj potencijalnoj jami (zidovi označavaju barijere u kojima je potencijalna energija beskonačna), dok je potencijalna energija unutar kutije jednaka nuli. Stoga, čestica ima samo kinetičku energiju:
Rješavanjem Schrödingerove jednadžbe za takvu česticu, lako je naći da vlastite funkcije u koordinatnoj i impulsnoj reprezentaciji definirana kao
i
- ,
gdje je . Varijanca (koja je korijen standardne devijacije) pozicije i količine gibanja računa se:
- .
Vidimo da je umnožak standardnih devijacija:
S obzirom na to da je najmanja moguća vrijednost vrijable upravo , nalazimo da je najmanji mogući umnožak standardnih devijacija količine gibanja i pozicije jednak
- .
S time pokazujemo da Heisenbergove relacije neodređenosti vrijede za česticu u kutiji. Do današnjeg dana nije pronađeno niti jedno odstupanje od Heisenbergovih relacija neodređenosti.
Kvantni harmonički oscilator[uredi | uredi kôd]

Jednodimenzionalni kvantni harmonički oscilator je kvantnomehanička varijantna klasičnoga harmoničkoga oscilatora. U tom slučaju, operatore količine gibanja i pozicije moguće je izraziti preko operatora podizanja i spuštanja:
- .
Pozivajući se na svojstva tih operatora,
- ,
trivijalno je odrediti varijancu,
Iz toga slijedi da je produkt standardnih devijacija količine gibanja i pozicije:
Što, kao što vidimo, zadovoljava Heisenbergove relacije neodređenosti.
Von Neumannov izvod Heisenbergovih relacija[uredi | uredi kôd]
Neka je:
- Hilbertov prostor,zajedno sa skalarnim produktom i normom , te sa kao operatorom identiteta u ;
- i samoadjungirani operatori u i , gdje je ;
- Te s normom .
Tada Heisenbergove relacije možemo izvesti u četiri koraka:
Korak 1:
Neka je
Stoga:
Što znači:
Pa iz Cauchy-Schwarzove nejednakosti slijedi:
Korak 2:
Neka su dva prozivoljna skalara, te definirajmo i . Stoga, općenito možemo zaključiti da vrijedi:
Korak 3:
Kao rezultat drugoga koraka, uz , i , imamo:
Korak 4:
Za slučaj kada je , dobivamo rezultat važan za kvantnu mehaniku, odnosno Heisenbergove relacije neodređenosti:
Interpretacija relacija neodređenosti[uredi | uredi kôd]
Interpretacija relacija neodređenosti bila je jedna od glavnih točaka prijepora između Bohra i Einsteina, naročito na petoj Solvayavoj konferenciji.[6] Po Kopenhagenskoj kvantnoj mehanici, ako dvije fizikalne veličine ne komutiraju, one nemaju istovremenu fizikalnu realnost. Što znači da ako poznajemo poziciju, količina gibanja nema realnost (tj. ne postoji). Također, ako čestici poznajemo komponentu spina u x-smjeru, to znači da čestica nema ostale komponente spina.[7] S druge strane, Einstein je to vidio kao naznaku nepotpunosti teorije, a ne kao znak da neke fizikalne veličine ne postoje ako znamo njihove konjugirane parove.[8]
Odnosi neodređenosti[uredi | uredi kôd]

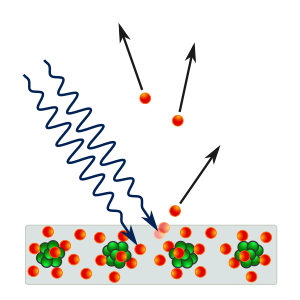
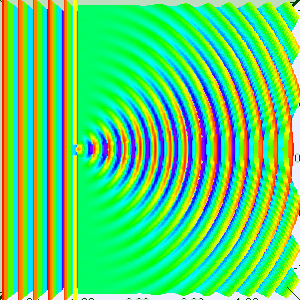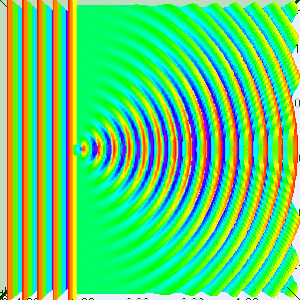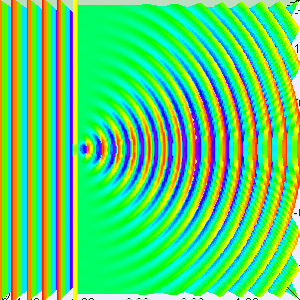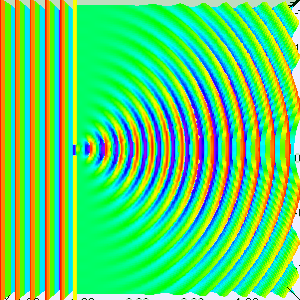







Klasična fizika prikazuje s jedne strane gibanje elektrona kao gibanje čestica uzduž određenih staza, s druge strane prikazuje širenje svjetlosti kao titranje kontinuuma. Ogib i interferencija elektronskih zraka, kao i pojava kvanata svjetlosti (fotona), sile nas da te temeljne klasične predodžbe podvrgnemo promjenama. Dok promatramo gibanje elektrona sve do u najsitnije potankosti kao gibanje čestica u točno određenim geometrijskim krivuljama, dok, dakle, gibanje elektrona shvatimo kao jedan astronomski sustav s točno određenim stazama, dotle u toj slici nema mjesta za valna svojstva. Isto tako, kad promatramo svjetlost kao elektromagnetski ili elastični val s određenim titrajima kontinuuma u svakom trenutku i u svakoj točki prostora ne možemo u tom kontinuiranom zbivanju otkriti ni traga takvim diskretnim kvantima svjetlosti. U stvarnosti, međutim, elektroni i svjetlost pokazuju valna i korpuskularna (čestica) svojstva (dualizam). To dokazuje da se ni klasična korpuskularna slika, ni klasična valna slika ne mogu dosljedno primijeniti na atomske procese. Opstojnost valnih svojstava materije ograničuje doseg korpuskularne slike, opstojnost kvanata svjetlosti ograničuje doseg klasične valne teorije. Temeljnim dualizmom vala i čestice, koji proniče čitavu nuklearnu fiziku, stavljene su granice klasičnoj fizici. Taj dualizam je ishodište kvantne kritike klasičnih zornih predodžbi. Kvantna teorija započinje tamo gdje zatajuju naše svakidašnje predodžbe o fizičkoj stvarnosti.
Do granica klasičnih predodžbi možemo najjasnije doći tako da iste fizičke procese opišemo u korpuskularnoj i valnoj slici. U klasičnoj mehanici gibanje neke točke potpuno je opisano ako u svaki pojedini trenutak znamo položaj i brzinu točke. Točno određena brzina, odnosno impuls sile, odgovara u valnoj slici valu s točno određenom valnom duljinom. Takav val s određenom valnom duljinom je ravni val, koji se širi po čitavom prostoru. Određena brzina elektrona ima, prema tome, u valnoj slici za posljedicu da je položaj elektrona u prostoru potpuno neodređen. Točno određenje mjesta i brzine elektrona stoji u suprotnosti s valnom predodžbom o gibanju materije. Želimo li u valnoj slici prikazati da se elektron nalazi u nekom malom području, moramo izgraditi jedan val koji snažno (intenzivno) titra samo u tom malom području, a izvan toga iščezava. Takav val nastaje po zakonima valnog širenja zbrajanjem vrlo mnogo ravnih valova različite duljine vala. Ti se ravni valovi u malom području pojačavaju, a izvan njega poništavaju. U korpuskularnoj slici valovima različite valne duljine odgovaraju različite brzine elektrona. Time što u valnoj slici ograničimo elektron na malo područje, brzina elektrona neminovno postaje neodređena. Što su manje dimenzije valnog paketa, to više treba valova s različitim valnim duljinama. Točno određenje mjesta u valnoj slici ima u korpuskularnoj slici za posljedicu potpunu neodređenost brzine. Želimo li gibanje elektrona istodobno prikazati kao širenje vala i kao gibanje čestica, u samom početku moramo se odreći mogućnosti da u najsitnije detalje provedemo obje predodžbe. Valna strana materije ukazuje na to da nema smisla govoriti istodobno o točno određenom položaju i brzini elektrona. Oba ta pojma mogu se primijeniti na elektron samo s izvjesnim stupnjem neodređenosti.
Na osnovu temeljnog dualizma postavit ćemo granice do kojih se pojmovi položaja i brzine smiju primijeniti na gibanje elektrona. Elektron neka se kreće na pravcu. Jednim mjerenjem je utvrđeno, da se on nalazi između točaka x i x + Δx. Rezultat toga mjerenja možemo u valnoj teoriji izraziti valom koji ima između x i x + Δx konačnu jakost (intenzitet), a izvan iščezava. Takav valni paket možemo prema zakonima valne teorije dobiti slaganjem ravnih valova s valnim duljinama od vrijednosti λ do vrijednosti λ + λ2/Δx.
Taj strogi matematički razultat je jasan ako pomislimo, da se ravni valovi moraju poništavati na granicama duljine Δx. U valnom paketu moraju se, dakle, pojavljivati ravni valovi, koji na granicama duljine Δx jedan ravni val učinio barem jedan titraj više od drugog vala. Prvi val neka je na toj duljini učinio n + 1 titraja (n je cijeli broj). Tada je njegova valna duljina jednaka Δx/(n + 1). Valna duljina drugog vala je jednaka λ = Δx/n, jer je taj drugi val učinio samo n titraja na duljini Δx. Prema tome, razlika u valnim duljinama između ta oba vala dana je razlikom:
Zaista vidimo da je valna duljina valova, koji izgrađuju valni paket, raspršena od vrijednosti λ do vrijednosti λ + λ2/Δx. Prema de Broglievu odnosu tim valnim duljinama odgovaraju impulsi između h/λ i h/(λ + Δλ). Raspršenje Δp impulsa dano je razlikom:
Uvrstimo li ovaio za raspon valne duljine gornju jednadžbu, dobivamo za raspršenje impulsa izraz:
Odatle proizlazi da je umnožak iz neodređenosti položaja Δx i neodređenosti impulsa Δp jednak Planckovoj konstanti h:
To je odnos neodređenosti, koju je izveo Heisenberg iz osnovnih zakona kvantne teorije. Ona izražava da je općenito nemoguće istovremeno točno ustanoviti brzinu i položaj elektrona. S obzirom na valna svojstva materije ne može se korpuskularna (čestica) slika točnije primjenjivati nego što to dopuštaju odnosi neodređenosti. Heisenbergovim odnosom neodređenosti nije isključeno da se pojedinačno odredi sasvim točno ili brzina ili položaj elektrona, ali kod točnog određenja jedne veličine druga veličina ostaje potpuno neodređena. Tako na primjer poznavanje elektrona s određenom brzinom isključuje mogućnost da bilo što detaljno izjavimo o njegovu položaju u prostoru. Govorimo li, naprotiv, o elektronu s brzinom između vrijednosti v i vrijednosti v + Δv, možemo elektronu pripisati položaj, utvrđen do na neizvjesnu duljinu, jednaku h/m∙Δv. Odnosi neodređenosti pogađaju samo istovremeno mjerenje brzine i položaja čestice, te određuje granice do kojih se korpuskularni pojmovi kao položaj i brzina mogu primjenjivati, a da ne nastupimo u sukob s pokusima ustanovljenim valnim svojstvima materije. Točnije primjenjivanje položaja i brzine kod atomskih procesa protivi se načelima kvantne teorije i ono bi iz paradoksa val-korpuskula stvorilo nerazrješivu logičku suprotnost.
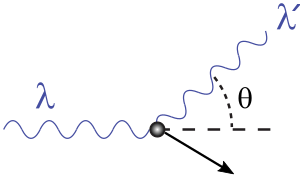
Ne može postojati ni jedan pokus u kojem bi istovremeno mogao točnije mjeriti položaj i impuls elektrona, nego što to dopuštaju odnosi neodređenosti. Heisenberg i Bohr su na nizu pokusa analizirali te fizičke odnose. Položaj elektrona na pravcu mogli bismo, u načelu, odrediti mikroskopom tako da obasjamo elektron svjetlošću vrlo male valne duljine. Po zakonima optike položaj je elektrona na pravcu neizvjestan za valnu duljinu upotrebljene svjetlosti. Tvrdim gama-zrakama dalo bi se postići vrlo točno određenje mjesta. Međutim, kvant svjetlosti, koji se od elektrona odbija (reflektira) k motritelju (fotografskoj ploči), daje prilikom sraza elektronu impuls u smjeru pravca. Taj preneseni impuls na elektron otprilike je jednako velik kao i prvotni impuls kvanta svjetlosti. Što je manja valna duljina svjetlosti, kojom obasjavamo elektron, to je veći impuls, što ga dobiva elektron prilikom sraza s kvantom svjetlosti. Upotrebom svjetlosti male valne duljine, doduše, možemo točno odrediti položaj elektrona na pravcu, ali tom svjetlošću male valne duljine znatno mijenjamo impuls elektrona. Što točnije odredimo položaj, to neizvjesniji postaje impuls elektrona. Neizvjesnost u položaju elektrona jednaka je valnoj duljini λ, neizvjesnost u impulsu elektrona prilikom obasjavanja jednaka je impulsu kvanta svjetlosti h/λ. Za umnožak neizvjesnosti mjesta Δx i neizvjesnost impulsa Δp prilikom mjerenja dobivamo zaista Planckovu konstantu h:
O postojanju odnosa neodređenosti osvjedočit ćemo se još na jednom primjeru. Položaj elektrona možemo vrlo strogo odrediti, ako pustimo katodne zrake kroz mali otvor na zastoru. Položaj elektrona u trenutku prolaza točnije je određen, što se uzme manji otvor. No pri tom nužno postaje neizvjestan njegov impuls. Uzmimo da je impuls katodnih zraka ispred zastora točno određen, što znači da se prema zastoru širi ravni val određene valne duljine. Ispred zastora je položaj elektrona sasvim neodređen. U trenutku prolaza je položaj elektrona fiksiran do na širinu d otvora u zastoru. No val, koji prolazi kroz otvor na zastoru, nužno skreće. Iza otvora dobivamo poznatu ogibnu sliku sa svijetlim i tamnim prstenovima. Val titra snažno (intenzivno) samo u kutnom području koje se prostire do granice, gdje nastupa prvo ugašenje vala:
Prenesimo to skretanje vala u korpuskularnu sliku. Impuls elektrona ne leži više točno u smjeru primarnih zraka, nego dobiva komponentu okomitu na prvobitni smjer. Komponenta impulsa u okomitom smjeru jednaka je:
Neizvjesnost položaja na osi y jednaka je širini otvora Δy = d. Neizvjesnost impulsa Δpy jednaka je 2∙py, jer elektron može biti raspršen na jednu ili drugu stranu osi y. Prema tome dobivamo:
Slični odnosi neodređenosti postoje i za valna svojstva materije. Granice korpuskularne slike našli smo imajući pred očima valna svojstva materije. Isto tako možemo odrediti granice klasične valne teorije imajući pred očima korpuskularna svojstva svjetlosti. Odnosi neodređenosti ostavljaju tada u zornoj valnoj teoriji mjesto za pojavu kvanta svjetlosti. Iz osnovnih načela kvantne teorije može se izvesti da se istodobno ne može govoriti o točnim vrijednostima električnoga i magnetskog polja. Za umnožak neodređenosti električnoga i magnetskog polja vrijede slični odnosi kao za položaj i brzinu elektrona.
Fizička stvarnost može se u makroskopskim dimenzijama predočiti korpuskularnom ili valnom slikom; u atomskim dimenzijama na svakoj od tih slika moramo izbrisati oštre linije i tako te, u makroskopskim dimenzijama suprotne slike, dovesti do međusobnog poklapanja.
Po kvantnoj teoriji klasični pojmovi gube djelomično svoj smisao u atomskim dimenzijama, a granice klasičnih predodžbi dane su odnosima neodređenosti. Dalje od tih granica ne dopire moć klasične fizike: u procesima u mikrosvijetu vladaju novi i nezorni zakoni kvantne teorije. Paradoksno ponašanje materije kao vala i čestice izraz je vlastite zakonitosti koja vlada u atomskim procesima. Ta dvojaka priroda materije ishodište je za kritiku klasičnih predodžbi.
Heisenbergovi odnosi neodređenosti onemogućuju da se na atomske staze primijeni u potpunosti klasični pojam staze. Kao staza u klasičnoj je mehanici određen niz uzastopnih položaja koje tijelo poprima u vremenskom slijedu. Gibanje planeta opisano je elipsom, a u svako vrijeme može se na elipsi odrediti točka u kojoj se nalazi planet. Gibanje mehaničkih predmeta određeno je ako u pojedinim trenucima poznamo njihov položaj i brzinu. Kako je s određenjem gibanja u nuklearnoj fizici? Odredimo li u jednom trenutku položaj elektrona, nipošto ne možemo reći gdje ćemo naći elektron u drugom kasnijem trenutku. Prilikom mjerenja položaja na takav smo nepredvidljiv način promijenili brzinu elektrona da je neizvjesno kuda će se kretati elektron poslije trenutka mjerenja. Osnovni dijelovi klasične staze, položaj i brzina, ostaju u kvantnoj fizici općenito neodređeni. Mjerenje atomskih procesa može se zorno tumačiti ili kao određenje mjesta ili kao određenje brzine. Dok u klasičnoj mehanici možemo niz takvih uzastopnih mjerenja ujediniti u stazu tijela u prostoru i vremenu, dotle u mikrosvijetu svako mjerenje ispoljuje kao radikalni zahvat u njegovu prirodu koji čini nemogućim povezivanje tih rezultata u stvarnu stazu elektrona. Kvantna diskontinuiranost onemogućuje isključivanje utjecaja motritelja na promatrani sustav i onemogućuje prijelaz k sve manjim smetnjama u sustavu prilikom mjerenja. Zahvati promatrača na atomski sustav uvijek su "veliki" i stvaraju novu fizikalnu situaciju u promatranom sustavu. Ne može se promatrati položaj elektrona, a da ga pri tome ne bombardiramo kvantima svjetlosti koji potpuno mijenjaju njegovu brzinu. Svako promatranje ostavlja u mikrosvijetu nepredvidljive promjene. Te promjene sprečavaju, da se rezultati mjerenja ujedine u klasičnu stazu. Na atomske procese može se prenijeti samo utoliko pojam staze koliko to dopuštaju odnosi neodređenosti. Ako ne prekoračujemo te granice dane osnovnim dualizmom vala i čestice, možemo gibanje elektrona približno opisati klasičnim stazama, a upotrebom toga klasičnog pojma dobit ćemo i u mikrosvijetu ispravne rezultate. Kod mnogih opisivanja atomskih procesa ne treba znati mjesto i brzinu elektrona točnije nego što to dopuštaju odnosi neodređenosti, i u tom slučaju možemo postići korpuskularnom ili valnom zornom slikom približno ispravne rezultate.
Na osnovu Heisenbergovih odnosa neodređenosti možemo promatrati dokle se dade primijenljiv pojam staze na gibanje elektrona u pojedinim stacionarnim stanjima atoma. Može se samo tada govoriti o stazi elektrona u pojedinom stacionarnom stanju ako se može odrediti niz točaka elektronske staze, a da pri tome ne promijenimo bitno energiju elektrona. Ako možemo mjeriti na primjer 10 točaka staze, tada već imamo priličan uvid u gibanje elektrona oko jezgre. Prilikom određenja tih točaka, naravno, ne smije biti znatno promijenjena energija elektrona tako da te sve točke mjerenja možemo pripisivati približno stacionarnom stanju iste energije. Promatrajmo najprije elektron u stabilnom stanju vodikova atoma. U stabilnom stanju kreće se elektron s energijom jednakom - R∙h na prosječnoj udaljenosti od 10−10 m od atomske jezgre. Da odredimo nekoliko točaka staze, trebamo svjetlost s valnom duljinom jednakom najviše 10−11 m. S tom svjetlošću možemo postići u određenju položaja točnost otprilike jednaku jednoj desetini promjera atoma. Međutim jedan kvant takve svjetlosti ima energiju tako veliku da je dovoljan jedan sraz između kvanta svjetlosti i elektrona pa da elektron bude potpuno izbačen iz atoma (Comptonov učinak). Od staze elektrona u najnižim stacionarnim stanjima možemo u pokusu promatrati samo jednu jedinu točku. Prema tome nema uopće smisla da pojam staze primijenimo na elektron u najnižim energetskim stanjima. Pojam određene elektronske staze dade se održati tek kod visokih stacionarnih stanja. U stacionarnim stanjima s kvantnim brojevima n ima atom za n2 veći promjer nego u stabilnom stanju; dakle, s kvantnim brojem n = 1 000 ima atom 1 000 000 puta veći promjer. Kod takvog stacionarnog stanja može se promatrati infracrvenom svjetlošću niz točaka staze, a da pri tome ne promijenimo bitno stacionarno stanje elektrona. Elektron prilikom sraza s kvantima svjetlosti, već prilično velike valne duljine, odnosno vrlo malog impulsa, stalno se kreće između 900-tog i 1100-tog stanja. Comptonovim učinkom tek se malo mijenja energija i brzina elektrona, pa elektron ostaje u susjednim stacionarnim stanjima. Sva stacionarna stanja ne razlikuju se znatno po svojim svojstvima, i prema tome mjerenje položaja elektrona možemo pripisivati stazi elektrona približno u 1000-tom stacionarnom stanju.
Kako vidimo, pojam staze dade se održati samo kod visokih stacionarnih stanja, gdje su dimenzije atoma velike i gdje su gusto nanizana stacionarna stanja. Prema niskim energijama elektrona naprotiv potpuno zatajuje klasični pojam staze. Klasičnim pojmovima dadu se približno ispravno opisati samo svojstva atoma za velike kvantne brojeve. Valjanost klasičnih pojmova kod visokih stacionarnih stanja izražava istu činjenicu kao i Bohrovo načelo korespondencije. Po načelu korespondencije za velike kvantne brojeve prelazi kvantna zakonitost u klasičnu. Na osnovu odnosa neodređenosti vidimo ponovo zašto primjenom klasičnih predstava na atome kod visokih stacionarnih stanja možemo s punim pravom govoriti o elektronu koji se kreće u određenoj stazi, na primjer u jednoj od Bohrovih kružnica. Dimenzije atoma za ta visoka stacionarna stanja su takve da se upotrebom korpuskularne klasične slike ne dospijeva u suprotnost s valnim svojstvima materije. Ako ne prekoračujemo granice dane Heisenbergovim odnosima neodređenosti, možemo na elektron primijeniti predstave i zakone klasične mehanike.
Bitno je za neprotuslovnost kvantne teorije da se kod nijednog pokusa istodobno ne mogu ustanoviti valna i korpuskularna svojstva. Pred pramen svjetlosti možemo postaviti zastor na kojemu se nalaze dvije rupice, vrlo blizu jedna uz drugu. Iza zastora na fotografskoj ploči tad se dobiva poznata ogibna slika, nastala interferencijom svjetlosti koja dolazi od obiju rupica. Dobivena ogibna slika je u svojoj geometrijskoj građi bitno različita od slike koju bi dobili puštajući svjetlost najprije kroz jednu, a zatim kroz drugu rupicu na zastoru. Ogibna slika iza dviju rupica na zastoru ne nastaje tako da se jednostavno prekriju ogibne slike pojedinih rupica, već je karakter nastale ogibne slike u bitnom određen time da je svjetlost istodobno prošla kroz obje rupice. Kod takvog pokusa ostaje potpuno sakrivena korpuskularna priroda svjetlosti. Odmah bismo došli u nerazmrsivo protuslovlje s promatranom pojavom kada bi kod toga pokusa promatrali svjetlost kao kvante svjetlosti. Shvatimo li svjetlost kao roj čestica, to bi pojedina čestica nužno prošla kroz jednu ili drugi rupicu. Međutim je za česticu, koja je prošla kroz jednu rupicu, potpuno bez značenja da li se nalazi još jedna rupica na zastoru. Ali tada otpada međusobna interferencija svjetlosti od obiju zastora, i na fotografskoj bi se ploči pojavila slika jednaka s onom da je svjetlost prošla najprije kroz jednu, a zatim kroz drugu rupicu na zastoru. Iz toga primjera najbolje razabiremo da dolazimo u nerješivu proturječnost ako kod ogibnih pojava upotrijebimo korpuskularnu sliku.
Granice klasične fizike nalaze se tamo, gdje se više ne mogu zanemariti učinci koje izazivlje svako promatranje u promatranom sustavu. Kada promatramo gibanje planeta, možemo potpuno zanemariti tlak svjetlosti na njihovu površinu, međutim svako obasjavanje atoma vodi do bitnih promjena u mikrosvijetu. Zbog diskontinuiranosti atomskog zbivanja ne mogu se smatrati izazvane promjene mjerenjem beskonačno male pa ukloniti. Sve promjene u atomskim procesima su jednako velike, jednako dalekosežne. Kvantna teorija dolazi na mjesto klasične kad postaju bitni utjecaji što ih svako promatranje vrši na atomski sustav.
Svaki pokusni zahvat u atomski sustav vezan je s neuklonivim smetnjama koje u stanovitoj mjeri čine neizvjesnim rezultat kasnijeg mjerenja. Smetnje na promatranom sustavu imaju odlučno značenje za kvantnu teoriju. Te smetnje onemogućuju da se točno utvrde klasične veličine sustava, kao na primjer položaj i brzina, te tako omogućuju svu paradoksnost dualizma vala i čestica. Kada bi se iz nekih pokusa moglo odrediti točno brzina i položaj elektrona, tada bi time bili ustanovljeni svi klasični elementi sustava i primjena kvantne teorije bila bi isključena. Neizvjesnost, koja ulazi u atomske sustave samim mjerenjem, označuje granice klasičnog promatranja i dopušta da se elektron kod jednog pokusa pojavi kao val, a kod drugog kao čestica. U svakom od tih pokusa izbrisane su neke klasične crte u valnoj, odnosno korpuskularnoj slici materije, a to oštećenje klasičnih sastavnih elemenata omogućuje da se svi ti pokusi ujedine u izraz jedinstvene fizikalne stvarnosti.
Mjerenjem unesena neizvjesnost u atomske sisteme sprečava da se na osnovu jednog pokusa odredi točan rezultat sljedećeg pokusa. U klasičnom načelu kauzalnosti je neophodno poznavanje brzine i položaja elektrona u jednom trenutku. No u nuklearnoj fizici ne samo da se nikada ne mogu istodobno točno mjeriti položaj i brzina elektrona, već bi njihova istodobna određenost izazvala nerazmrsivu suprotnost. Zajedno s klasičnim predstavama položaja i brzine u atomskoj se fizici pokazuje neprikladnim i klasično načelo kauzalnosti. Budući da smetnje kod pokusa proizvode izvjesnu neodređenost u atomskom sustavu, to se na osnovu jednog pokusa može zaključiti samo na vjerojatnost ishoda daljih pokusa. Ako u jednom kasnijem pokusu ispitujemo fizikalnu veličinu, koja nije smetana prethodnim pokusom, možemo strogo odrediti ishod pokusa. U tom slučaju su pokusi kauzalno povezani. Tako su zakoni kvantne teorije djelomično statističkog i determiniranog karaktera, oni se nadopunjuju kao dva razna načina promatranja. Kao i u kinetičkoj teoriji materije, tako se i u kvantnoj fizici služimo statistikom kada više ne možemo primijeniti strogo kauzalno promatranje. Nezavisno od te neizvjesnosti u slijedu pokusa postoje u kvantnoj teoriji strogi zakoni iz kojih se mogu proračunati atomske veličine. Opstojnost tih strogih zakona kvantne teorije nazvao je Bohr načelom kauzalnosti kvantne fizike. Stroga determiniranost kvantne teorije pogađa više vrijednosti atomskih veličina, na primjer energije, momente vrtnje i tako dalje, negoli slijed pokusa koja proniče neminovna neizvjesnost.
Gradivo, na kojem se izgrađuje kvantna teorija, zorni su rezultati mjerenja. Sva ta najrazličitija mjerenja atomskih procesa mora kvantna teorija ujediniti u jedinstveni fizikalni sustav. U klasičnoj fizici sva se ta promatranja daju ujediniti u svojstva očiglednog događanja u prostoru i vremenu, kao na primjer gibanje planeta ili širenje valova po vodi. Makroskopske predmete možemo uzastopno podvrći nizu pokusa, i sve rezultate mjerenja tumačiti kao svojstva tih predmeta koji se nisu bitno promijenili u trenutku mjerenja. Atome ne možemo izravno primijetiti našim osjetilima kao predmete svakidašnjeg života. Do nas dopiru mikroprocesi samo po svojim vidljivim učincima. Atomske procese moramo promatrati uvijek u određenim spravama za pokus, moramo ih utvrditi uvijek u čvrstom makroskopskom okviru. Rezultat pojedinog pokusa uvijek se da zorno tumačiti nekom klasičnom slikom. Takvi pokusi, koje tumačimo zornim predstavama klasične, makroskopske fizike, jedino su što znamo o atomima. Rezultati mjerenja atomskih procesa međutim se ne mogu tako potpuno ujediniti u zornu sliku predmeta kao u klasičnoj fizici. Treba se samo sjetiti, da se materija jedanput pojavljuje kao val, a drugi put kao korpuskula. Ovaj temeljni dualizam nas sprečava da elektron shvatimo kao predmet nalik na zornu česticu ili zorni val. Takav, kakav se prikazuje u pokusu, ne dopušta nam mikrosvijet da na osnovu njegovih makroskopskih (vidljivih) učinaka izgradimo jednoznačnu sliku objekta kojih promjene u prostoru i vremenu bi imale za posljedicu promatranja pokusa. Atomski procesi su općenito nezornog karaktera, naš svakidašnji govor nije sposoban dati potpuno odgovarajuću sliku događanja u mikrosvijetu. Ne možemo ni očekivati da će slike i pojmovi, stečeni u svakidašnjem iskustvu s makroskopskim predmetima, zadržati valjanost i u mikrosvijetu.[10]
Izvori[uredi | uredi kôd]
- ↑ Heisenberg, W. 21. ožujka 1927. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift für Physik. 43 (3–4): 172–198. doi:10.1007/BF01397280
- ↑ Trabesinger, A. History of quantum mechanics: The path to agreement. Nature Physics. 4: 349. doi:doi:10.1038/nphys950 Provjerite vrijednost parametra
|doi=(pomoć) - ↑ Heisenbergove relacije neodređenosti, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2019.
- ↑ a b L.D. Landau, E.M. Lifshitz. 1977. Quantum Mechanics: Non-Relativistic Theory. Vol. 3 3rd izdanje. Pergamon Press. ISBN 978-0-08-020940-1
|volume=sadrži dodatni tekst (pomoć) Online copy. - ↑ Hilgevoord, Jan. 1998. The uncertainty principle for energy and time. II. American Journal of Physics. 66 (5): 396–402. doi:10.1119/1.18880
- ↑ Mehra, J. 1987. Niels Bohr's discussions with Albert Einstein, Werner Heisenberg, and Erwin Schrödinger: The origins of the principles of uncertainty and complementarity. Foundations of Physics. 17 (5): 461–506. doi:10.1007/BF01559698
- ↑ Bohr N. Discussions with Einstein on Epistemological Problems in Atomic Physics. The Value of Knowledge: A Miniature Library of Philosophy. Marxists Internet Archive. Pristupljeno 9. siječnja 2016. From Albert Einstein: Philosopher-Scientist (1949), publ. Cambridge University Press, 1949. Niels Bohr's report of conversations with Einstein.
- ↑ Paul Arthur Schilpp. Albert Einstein: Philosopher Scientist, Tudor Publishing Company (1951), str. 672.
- ↑ F. Dorn, F. Bader: Physik-Oberstufe. Schroedel, Hannover 1986, ISBN 3-507-86205-0.
- ↑ Ivan Supek: "Nova fizika", Školska knjiga Zagreb, 1966.


![{\displaystyle [{\hat {x}},{\hat {p}}]=i\cdot \hbar }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cde645a39896ae1cbcd94204dccd08ce413f5ec)














![{\displaystyle \operatorname {P} [a\leq X\leq b]=\int _{a}^{b}|\psi (x)|^{2}\,\mathrm {d} x~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8852ff1f2e7c518fce8dfbb77f8e8a7920c63f3)






![{\displaystyle [{\hat {A}},{\hat {B}}]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3133da214f8f0fcf1ba11e907cfd121a2179b1b4)
![{\displaystyle [{\hat {x}},{\hat {p}}]=i\hbar .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fee0861ae7784cb51a1b43f6c51735c22c23274e)


![{\displaystyle [{\hat {x}},{\hat {p}}]|\psi \rangle =({\hat {x}}{\hat {p}}-{\hat {p}}{\hat {x}})|\psi \rangle =({\hat {x}}-x_{0}{\hat {I}}){\hat {p}}\,|\psi \rangle =i\hbar |\psi \rangle ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8255257353e4743e966c106dea5674689ed04690)

![{\displaystyle [{\hat {x}},{\hat {p}}]|\psi \rangle =i\hbar |\psi \rangle \neq 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04d341bbd1c29d8f96a5ce5ad6e2cf856d1b1f40)
![{\displaystyle [{L_{x}},{L_{y}}]=i\hbar \epsilon _{xyz}{L_{z}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d32a97397e35b96330795406f1a55f6c5acfef2d)

![{\displaystyle [S_{i},S_{j}]=i\hbar \varepsilon _{ijk}S_{k}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4dedf5de9d2b4259facf15dd9c85a31ecbab75e)



























![{\displaystyle [{\hat {A}},{\hat {B}}]=a\mathbf {1} _{\mathcal {H}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b006c358f05b75b50a1be7a59660b5d4a2232ef)




![{\displaystyle =\mathrm {i} \cdot \langle ({\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}})\psi ,\psi \rangle =\mathrm {i} \cdot \langle [{\hat {A}},{\hat {B}}]\psi ,\psi \rangle =\mathrm {i} \cdot \langle a\mathbf {1} _{\mathcal {H}}\psi ,\psi \rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c183cb95396f0dce9e540a1d25aec3c96773e73d)























