Joseph-Louis Lagrange: razlika između inačica
| Redak 30: | Redak 30: | ||
Lagrange je s 19 godina postao je [[profesor]] matematike na artiljerijskoj školi u Torinu i ubrzo se proslavio metodom obradbe problema iz računa varijacija uvodeći pojam varijacije ''δy'' neke [[Funkcija (matematika)|funkcije]] (1759.). Prvom razdoblju njegova rada pripadaju i istraživanja o [[Libracija|libraciji]] [[Mjesec]]a (1764.) i teoriji gibanja [[Jupiterovi prirodni sateliti|Jupiterovih satelita]] (1766.), za što je dobio nagradu Francuske akademije. |
Lagrange je s 19 godina postao je [[profesor]] matematike na artiljerijskoj školi u Torinu i ubrzo se proslavio metodom obradbe problema iz računa varijacija uvodeći pojam varijacije ''δy'' neke [[Funkcija (matematika)|funkcije]] (1759.). Prvom razdoblju njegova rada pripadaju i istraživanja o [[Libracija|libraciji]] [[Mjesec]]a (1764.) i teoriji gibanja [[Jupiterovi prirodni sateliti|Jupiterovih satelita]] (1766.), za što je dobio nagradu Francuske akademije. |
||
Godine 1767. postao je predsjednik [[berlin]]ske Akademije, gdje je ostao do 1787., kada se odazvao pozivu [[Luj XVI., kralj Francuske| |
Godine 1767. postao je predsjednik [[berlin]]ske Akademije, gdje je ostao do 1787., kada se odazvao pozivu [[Luj XVI., kralj Francuske|Luja XVI., kralja Francuske]] da dođe u [[Pariz]]. Berlinskomu razdoblju pripadaju i istraživanja o verižnim razlomcima i njihovoj primjeni u rješavanju [[Diofantska jednadžba|diofantskih jednadžbi]] 1. i 2. stupnja, zatim istraživanja o problemu algebarske rješivosti [[Algebra|algebarskih jednadžbi]] (1770.), pri čem se služio ispitivanjem ponašanja nekih racionalnih funkcija korijena promatrane jednadžbe pri međusobnom permutiranju tih korijena. Tako je utro putove koji će dovesti do [[Teorija grupa|teorije grupa]] ([[Évariste Galois]]), a 1772. uspio je naći neka partikularna rješenja problema triju tijela. Bavio se i [[Hidrodinamika|hidrodinamikom]]; 1781. izveo izraz za brzinu valova u plitkim kapljevinama. |
||
Godine 1788. pošto se Lagrange preselio u Pariz, izišlo je njegovo fundamentalno djelo iz područja [[mehanika|teorijske mehanike]] ''Analitička mehanika'' ([[Francuski jezik|fra]]. ''Mécanique analytique''). Godine 1793. bio je postavljen za predstojnika Komisije za utege i mjere u Parizu, a 1797. za profesora na ''École polytechnique''. Nezadovoljan dotadašnjim načinom definiranja osnovnih pojmova [[Infinitezimalni račun|infinitezimalnoga računa]], Lagrange ga je pokušao izgraditi bez pomoći pojma beskonačno malih veličina, polazeći od pretpostavke mogućnosti razvijanja zadane funkcije u red [[potencija]], i s pomoću koeficijenata tog razvoja odredio je [[Derivacija|derivacije]] različitog reda. Iako je u provedbi tih ideja katkad nedostajalo strogosti, one su se pokazale vrlo plodnima, osobito pri izgradnji teorije funkcija jedne i više kompleksnih varijabla tijekom 19. i 20. stoljeća. |
Godine 1788. pošto se Lagrange preselio u Pariz, izišlo je njegovo fundamentalno djelo iz područja [[mehanika|teorijske mehanike]] ''Analitička mehanika'' ([[Francuski jezik|fra]]. ''Mécanique analytique''). Godine 1793. bio je postavljen za predstojnika Komisije za utege i mjere u Parizu, a 1797. za profesora na ''École polytechnique''. Nezadovoljan dotadašnjim načinom definiranja osnovnih pojmova [[Infinitezimalni račun|infinitezimalnoga računa]], Lagrange ga je pokušao izgraditi bez pomoći pojma beskonačno malih veličina, polazeći od pretpostavke mogućnosti razvijanja zadane funkcije u red [[potencija]], i s pomoću koeficijenata tog razvoja odredio je [[Derivacija|derivacije]] različitog reda. Iako je u provedbi tih ideja katkad nedostajalo strogosti, one su se pokazale vrlo plodnima, osobito pri izgradnji teorije funkcija jedne i više kompleksnih varijabla tijekom 19. i 20. stoljeća. |
||
Inačica od 19. srpnja 2021. u 22:46
| Joseph-Louis Lagrange | |
 | |
| Rođenje | 25. siječnja 1736. rođen kao Giuseppe Lodovico Lagrangia Torino, Italija |
|---|---|
| Smrt | 10. travnja 1813. Pariz, Francuska |
| Prebivalište | Kraljevina Sardinija Francuska Prusija |
| Državljanstvo | Englesko |
| Narodnost | Talijan |
| Polje | Matematička analiza, teorija brojeva, klasična mehanika, nebeska mehanika |
| Institucija | Berlinska Akademija Komisija za utege i mjere u Parizu École polytechnique u Parizu |
| Akademski mentor | Leonhard Euler |
| Poznat po | Lagrangeove jednadžbe gibanja, Lagrangeova funkcija ili lagrangian, Lagrangeove točke ili točke libracije |
| Portal o životopisima | |
Joseph-Louis Lagrange (Torino, 25. siječnja 1736. - Pariz, 10. travnja 1813.), talijanski matematičar i astronom, živio je u doba prosvjetiteljstva. Napravio je znatne doprinose na polju matematičke analize, teorije brojeva, klasične mehanike i nebeske mehanike.
Životopis
Lagrange je s 19 godina postao je profesor matematike na artiljerijskoj školi u Torinu i ubrzo se proslavio metodom obradbe problema iz računa varijacija uvodeći pojam varijacije δy neke funkcije (1759.). Prvom razdoblju njegova rada pripadaju i istraživanja o libraciji Mjeseca (1764.) i teoriji gibanja Jupiterovih satelita (1766.), za što je dobio nagradu Francuske akademije.
Godine 1767. postao je predsjednik berlinske Akademije, gdje je ostao do 1787., kada se odazvao pozivu Luja XVI., kralja Francuske da dođe u Pariz. Berlinskomu razdoblju pripadaju i istraživanja o verižnim razlomcima i njihovoj primjeni u rješavanju diofantskih jednadžbi 1. i 2. stupnja, zatim istraživanja o problemu algebarske rješivosti algebarskih jednadžbi (1770.), pri čem se služio ispitivanjem ponašanja nekih racionalnih funkcija korijena promatrane jednadžbe pri međusobnom permutiranju tih korijena. Tako je utro putove koji će dovesti do teorije grupa (Évariste Galois), a 1772. uspio je naći neka partikularna rješenja problema triju tijela. Bavio se i hidrodinamikom; 1781. izveo izraz za brzinu valova u plitkim kapljevinama.
Godine 1788. pošto se Lagrange preselio u Pariz, izišlo je njegovo fundamentalno djelo iz područja teorijske mehanike Analitička mehanika (fra. Mécanique analytique). Godine 1793. bio je postavljen za predstojnika Komisije za utege i mjere u Parizu, a 1797. za profesora na École polytechnique. Nezadovoljan dotadašnjim načinom definiranja osnovnih pojmova infinitezimalnoga računa, Lagrange ga je pokušao izgraditi bez pomoći pojma beskonačno malih veličina, polazeći od pretpostavke mogućnosti razvijanja zadane funkcije u red potencija, i s pomoću koeficijenata tog razvoja odredio je derivacije različitog reda. Iako je u provedbi tih ideja katkad nedostajalo strogosti, one su se pokazale vrlo plodnima, osobito pri izgradnji teorije funkcija jedne i više kompleksnih varijabla tijekom 19. i 20. stoljeća.
Lagrangeove točke
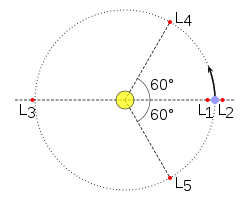
Lagrangeove točke ili točke libracije, stabilne su točke u problemu interakcije triju tijela (npr. Sunce, planet i neka treća masa). Općenito, problem triju (i više) tijela nije moguće analitički riješiti. Postoji 5 takvih točaka, koje je odredio Lagrange. Tri od njih su na spojnici Sunce–planet: L1 između Sunca i planeta, L2 s one strane planeta, L3 s one strane Sunca. L4 i L5 nalaze se pod kutom od 60°, gledano sa Sunca, ispred i iza planeta na njegovoj stazi. Trojanci su planetoidi ili prirodni sateliti koji dijele putanju s planetom ili nekim većim satelitom i gibaju se ispred ili iza njega pod kutom od približno 60° (Trojanci i veće tijelo nalaze se u vrhovima istostraničnoga trokuta). Njihovo je gibanje stabilno. Položaj Trojanaca odgovara Lagrangeovim točkama stabilnosti L4 i L5 u Lagrangeovu rješenju problema triju tijela. Prvi otkriveni Trojanci bili su na Jupiterovoj putanji. Oni koji kruže oko Sunca ispred Jupitera nazvani su imenima osvajača Troje, a oni iza Jupitera imenima njezinih branitelja. Prvi je otkriven Ahilej, najveći je Hektor. Vrlo su tamni, malog albeda, a ima ih više stotina tisuća s promjerom većim od 1 km. Poznato je da Mars ima tri Trojanca, Neptun osam, a 2010. otkriven je i Zemljin Trojanac (2010 TK7), promjera oko 300 m. Kruži oko Sunca u Lagrangeovoj točki ispred Zemlje. Saturn ima nekoliko trojanskih satelita: npr. putanju s Tetijom dijele njezini Trojanci Telesta i Kalipsa, a s Dionom Helena i Polideuk.[1]
