Normalna raspodjela
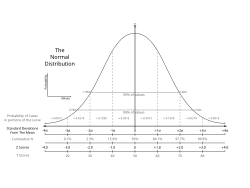
Gaussova krivulja još se naziva i normalna raspodjela, te se primjenjuje u raznim prirodnim znanostima, kao i u znanostima koje se bave proučavanjem ponašanja. Mnoštvo rezultata psiholoških testova i fizičkih pojava, slijede normalnu raspodjelu. Iako su često temeljni uzroci fenomena za koje se raspodjela upotrebljava nepoznati, normalna raspodjela primjenjuje se kada rezultat oblikuje mnoštvo manjih efekata. Uz to, normalna raspodjela je vrlo važna raspodjela vjerojatnosti u mnogim područjima. Svakome tko se ikad susreo sa statistikom, poznata je čuvena Gaussova krivulja, uobičajen model za prikaz varijacija. Ona govori o prirodi nasumičnosti, a predstavlja Gaussovu ili normalnu raspodjelu. Smisao je u tome da stvari kad se mijenjaju, nastoje ostati u blizini točke prosjeka, pa se raspoređuju oko tog prosjeka po glatkoj, zvonolikoj krivulji. Gaussova, ili normalna krivulja je unimodalna, ima oblik zvona i proteže se od - do. Krivulja je simetričnog oblika. Nema nultočaka, jer nikada ne presijeca os x, nego joj se samo približava. Specifičnost krivulje je ta što se 50 % podataka za koje se krivulja crta nalazi na jednoj strani krivulje, dok je ostalih 50 % podataka na drugoj strani.
Formula Gaussove funkcije je Zove se i funkcija gustoće normalne slučajne varijable (slučajne promjenjive) i primjenjuje se u vjerojatnosti.

