Hammingova udaljenost
 |
 |
 |
 |
U teoriji informacije, Hammingova udaljenost dvaju stringova jednake duljine je broj pozicija u kojima su odgovarajući simboli različiti. Drugim riječima, mjeri minimalni broj supstitucija potreban za promjenu jednog u drugo, ili broj grešaka koji je jedan string transformirao u drugi.
Na primjer:
- Hammingova udaljenost između 1011101 i 1001001 je 2.
- Hammingova udaljenost između 1011101 i 1001001 je 2.
- Hammingova udaljenost između 2143896 i 2233796 je 3.
- Hammingova udaljenost između "toned" i "roses" je 3.
Posebna svojstva[uredi | uredi kôd]
Za fiksnu duljinu n, Hammingova je udaljenost metrika vektorskog prostora riječi te duljine, jer očito ispunjava uvjete nenegativnosti, identitete neprimjetnih (indiscernibles) i simetrije, a i može se lako dokazati potpunom indukcijom da također zadovoljava nejednakost trokuta. Hammingova udaljenost između riječi a i b se također može shvatiti kao Hammingova težina od a−b, za prikladan izbor − operatora.
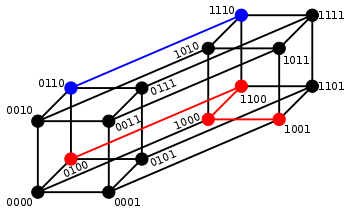
Za binarne stringove a i b Hammingova je udaljenost jednaka broju jedinica u a xor b. Metrički prostor od duljina-n binarnih stringova, zajedno s Hammingovom udaljenošću, je poznat kao Hammingova kocka - ekvivalentan je kao metrički prostor skupu udaljenosti vrhova grafa hiperkocke. Binarni string duljine n se također može shvatiti kao vektor u tretirajući svaki simbol stringa kao realnu koordinatu - ovim ugrađivanjem stringovi oblikuju vrhove n-dimenzionalne hiperkocke i Hammingova udaljenost stringova je jednaka Manhattan udaljenosti vrhova.
Povijest i primjene[uredi | uredi kôd]
Hammingova udaljenost je imenovana po Richardu Hammingu, koji ju je uveo u svom fundamentalnom radu o kodovima detekcije i ispravljanja grešaka (1950.). Koristi se u telekomunikacijama za brojenja broja obrnutih bitova binarne riječi fiksne duljine kao procjenu grješke, i stoga se ponekad zove signalna udaljenost. Analiza bitova Hammingovom težinom se koristi u nekoliko područja uključujući teoriju informacije, teoriju kodiranja i kriptografiju. Međutim, za uspoređivanje stringova različitih duljina, ili stringova u kojima se očekuju ne samo supstitucije već i umetanja i brisanja, prikladnija je složenija metrika kao što je Levenshteinova udaljenost.
Primjer algoritma[uredi | uredi kôd]
Python funkcija hamdist() računa Hammingovu udaljenost između dva stringa (ili "sekvencijalnih objekata" preslikanih u stringove) jednake duljine.
def hamdist(s1, s2):
assert len(s1) == len(s2)
return sum(z1 != z2 for z1, z2 in zip(s1, s2))
Sljedeća C++ funkcija računa Hammingovu udaljenost dvaju cijelih brojeva (smatranih binarnim vrijednostima, tj. slijedovima bitova). Vrijeme je proporcionalno Hammingovoj udaljenosti, radije nego broju bitova ulaza.
int hamudalj(int x, int y)
{
int udalj = 0, vrij = x^y;
while(vrij)
{
++udalj;
vrij &= vrij - 1;
}
return udalj;
}
Izvori[uredi | uredi kôd]
Djelimice prilagođeno iz Federal Standard 1037C.
Richard W. Hamming. Error Detecting and Error Correcting Codes, Bell System Technical Journal 26(2):147-160, 1950.

