Peterokut

Pravilni peterokut

Peterokut je svaki geometrijski lik koji se sastoji od pet kuteva. Zbroj kutova peterokuta iznosi 540°.

Pravilni peterokut

Kod pravilnog peterokuta sve stranice iste su duljine, svaki kut peterokuta ima 108° (5x108 = 540)

Površina pravilnog peterokuta stranice t računa se po sljedećoj formuli:

$P={\frac {t^{2}{\sqrt {25+10{\sqrt {5}}}}}{4}}={\frac {5t^{2}\tan(54^{\circ })}{4}}\approx 1.720477401t^{2}.$

Konstrukcija pravilnog peterokuta

Konstrukcija pravilnog peterokuta upisanog u krug uči se u osnovnoj školi pomoću šestara.

Konstrukcija pravilnog peterokuta, vrhovi na kružnici

Animirani GIF postupka konstrukcije pravilnog peterokuta upisanog u krug

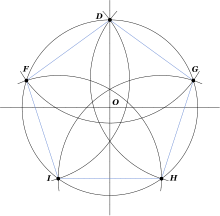
Nedovršeni članak Peterokut koji govori o geometriji treba dopuniti. Dopunite ga prema pravilima Wikipedije.