Bestežinsko stanje
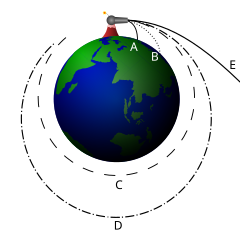
Bestežinsko stanje je stanje fizikalnog tijela na koje prividno ne djeluje sila teže (gravitacija). U takvu se stanju nalaze astronauti i svi predmeti u svemirskoj letjelici za vrijeme leta oko Zemlje takozvanom prvom kozmičkom brzinom ili 7,91 km/s. Zbog djelovanja centrifugalne sile poništava se djelovanje Zemljine gravitacije, pa u svemirskoj letjelici tijela i predmeti nemaju težinu, već lebde u prostoru bez obzira na svoju masu (na primjer zrnce prašine, kap vode, čovjek). Tijekom dvaju letova Poljakov je proveo u svemiru ukupno 678 dana, 16 sati i 58 minuta.[1]
Učinci[uredi | uredi kôd]
Jedna od posljedica bestežinskog stanja je nestanak istjecanja tekućina iz svojih spremnika, što uzrokuje znatne teškoće kod smještaja tekućeg raketnog goriva i njegovog napajanja raketnih motora.

U bestežinskom stanju nema uzgona, stoga prestaje i konventivni prijenos tvari i topline, što u slučaju plamena znači da postaje kuglast.

Dosadašnji višemjesečni letovi astronauta pokazali su da bestežinsko stanje u pogledu fizioloških i bioloških učinaka nije nepremostiva teškoća i da se sustavnim treningom živi organizmi mogu osposobiti da i dulje vrijeme izdrže to fiziološki neprirodno stanje. Svjetski rekord neprekidnog boravka u bestežinskom stanju drži ruski astronaut i liječnik Valerij Poljakov, koji je u orbitalnoj postaji Mir ostvario misiju u trajanju 437 dana, 17 sati i 58 minuta (od 8. siječnja 1994. do 20. ožujka 1995). Tijekom dvaju letova Poljakov je u svemiru proveo ukupno 678 dana, 16 sati i 58 minuta.[1]
Izvori[uredi | uredi kôd]
- ↑ a b Bestežinsko stanje. Hrvatska enciklopedija. Pristupljeno 15. siječnja 2024.
