Kvadratna jednadžba

Pod kvadratnom jednadžbom podrazumijevamo jednadžbu u kojoj se nepoznata veličina pojavljuje pod znakom potencije 2, dakle jednadžbu općenitog oblika

$ax^{2}+bx+c=0\,$

koja ustvari predstavlja poseban slučaj polinoma n-tog reda gdje je n=2.

Kvadratna jednadžba

Kvadratna jednadžba gdje je b=0

Kvadratnu jednadžbu gdje je b=0 možemo prikazati u obliku

$ax^{2}+c=0\,$ iz čega slijedi da je

$x^{2}=-{\frac {c}{a}}\,$

Ukoliko je jedan od članova negativan, jednadžba će imati dva realna rješenja (govorimo i o realnim korijenima kvadratne jednadžbe)

$x_{1}=+{\sqrt {\frac {c}{a}}},x_{2}=-{\sqrt {\frac {c}{a}}}\,$,

a ukoliko su oba člana negativna ili pozitivna jednadžba će imati dva imaginarna rješenja

$x_{1}=+i{\sqrt {\frac {c}{a}}},x_{2}=-i{\sqrt {\frac {c}{a}}}\,$.

Kvadratna jednadžba gdje je c=0

Kvadratnu jednadžbu gdje je c=0 možemo prikazati u obliku

$ax^{2}+bx=0\,$

što se može prikazati i kao

$x(ax+b)=0\,$.

Rješenja ove jednadžbe bit će očito

$x_{1}=0,x_{2}=-{\frac {b}{a}}\,$,

gdje ovakav oblik kvadratne jednadžbe ima uvijek realna rješenja.

Kvadratna jednadžba sa svim članovima

Kvadratna jednadžba sa svim članovima oblika

$ax^{2}+bx+c=0\,$

može se jednostavno riješiti ukoliko se kvadratna jednadžba može prikazati kao produkt dva binomna faktora. Na primjer, odmah je vidljivo da se jednadžba

$x^{2}+x-12=0\,$

može prikazati i kao

$(x-3)(x+4)=0\,$

gdje je očito da će rješenja jednadžbe biti

$x_{1}=3,x_{2}=-4\,$

jer upravo za te vrijednosti nezavisne varijable vrijednost funkcije će biti jednaka nuli. Kvadratna jednadžba se, međutim, pojavljuje u tako povoljnim oblicima razmjerno rijetko te najčešće valja poznavati općenito rješenje kvadratne jednadžbe.

Općenito rješenje kvadratne jednadžbe

Kvadratna jednadžba oblika

$ax^{2}+bx+c=0\,$

može se transformirati redom kako slijedi

$x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0\,$

$(x+{\frac {b}{2a}})^{2}+{\frac {c}{a}}-{\frac {b^{2}}{4a^{2}}}=0\,$

$(x+{\frac {b}{2a}})^{2}={\frac {b^{2}}{4a^{2}}}-{\frac {c}{a}}\,$

$(x+{\frac {b}{2a}})^{2}={\frac {b^{2}-4ac}{4a^{2}}}\,$

$x_{1,2}+{\frac {b}{2a}}=\pm {\sqrt {\frac {b^{2}-4ac}{4a^{2}}}}$

$x_{1,2}=-{\frac {b}{2a}}\pm {\sqrt {\frac {b^{2}-4ac}{4a^{2}}}}$

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\,$

gdje posljednja jednakost daje eksplicitna rješenja kvadratne jednadžbe. Izraz

$b^{2}-4ac\,$

nazivamo diskriminantom kvadratne jednadžbe te kvadratnu jednadžbu možemo prikazati i u slijedećem obliku

$x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}.\,$

Diskriminanta i rješenja kvadratne jednadžbe

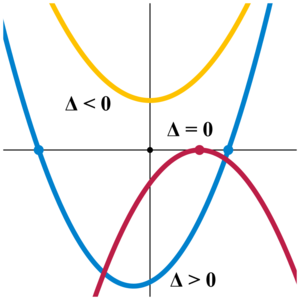
Kvadratna jednadžba samo je jedan poseban slučaj kvadratne funkcije:

$y=ax^{2}+bx+c\,$

gdje je ona za rješenja kvadratne jednadžbe $x_{1}$ i $x_{2}$ jednaka nuli. Postojanje rješenja je neposredno uvjetovano tijekom i osobinama kvadratne funkcije. Ukoliko je diskriminanta D>0 (slika desno, D =$\bigtriangleup$, krivulja obojena u plavo) tada će kvadratna jednadžba imati dva realna rješenja, ukoliko je diskriminanta D=0, kvadratna jednadžba će imati jedno, dvostruko rješenje (crvena krivulja), a ukoliko je diskriminanta D<0 tada jednadžba nema realnih već ima dva konjugirano-kompleksna rješenja (žuta krivulja).

Rješenja kvadratne jednadžbe imaju i neka posebna svojstva data Vieteovim poučkom koji ustanovljava slijedeću povezanost s koeficijentima jednadžbe a, b i c:

$x_{1}+x_{2}=-{\frac {b}{a}}$ te

$x_{1}x_{2}={\frac {c}{a}}$.

Kvadratna funkcija i kvadratna jednadžba

Kvadratnu jednadžbu možemo shvatiti i kao poseban slučaj kvadratne funkcije y=f(x) za vrijednost funkcije y=0, gdje tada rješenja kvadratne jednadžbe predstavljaju nulišta kvadratne funkcije i nul točke grafa funkcije. Parabola je u tom slučaju krivulja koja predstavlja graf kvadratne funkcije, a razlikujemo tri slučaja:

1/ Ukoliko postoje dva različita sjecišta grafa funkcije s apscisom, odn. x-osi koordinatnog sustava, kvadratna jednadžba će imati dva različita i realna rješenja,

2/ Ukoliko je apscisa, odn. x-os tangenta grafa kvadratne funkcije te prolazi kroz tjeme parabole, kvadratna jednadžba će imati jedno dvostruko i realno rješenje, te

3/ Ukoliko graf kvadratne funkcije nigdje ne siječe apscisu, odn. x-os, tada kvadratna jednadžba nema realna, već ima dva konjugirano-kompleksna rješenja.

Značaj

U fizikalnim sustavima brojne veličine ovise o kvadratu drugih veličina te kvadratnu jednadžbu često nalazimo ne samo u matematici nego i u vrlo praktičnoj primjeni. Na primjer, centrifugalna sila razmjerna je kvadratu obodne brzine, električna snaga na električnom otporniku razmjerna je kvadratu električnog napona koji postoji na njegovim priključcima, pri jednoliko ubrzanom gibanju prijeđeni put je razmjeran kvadratu vremena i td.

Literatura

• Gusić J., Mladinić P., Pavković B., "Matematika 2", Školska knjiga, Zagreb, 2006.