Ubrzanje Zemljine sile teže




Ubrzanje Zemljine sile teže, ubrzanje sile teže, ubrzanje slobodnog pada ili gravitacijsko ubrzanje (oznaka: g) je ubrzanje slobodnog pada u gravitacijskom polju Zemlje. Srednja vrijednost na površini Zemlje (razini mora) iznosi oko 9,81 m/s², a zbog vrtnje i spljoštenosti Zemlje (geoid) mijenja se sa zemljopisnom širinom. Dogovorom utvrđena standardna vrijednost od 9,80665 m·s−2 koristi se kao fizikalna konstanta i mjerna jedinica, a označava se kao gn, g0 ili g.
Isaac Newton je povezao Galilejeve zakone gibanja s Keplerovim zakonima o kretanju planeta i, uvevši mehaničku silu u astronomiju, izveo opći zakon privlačenja masa (1681.) ili poznatiji kao Newtonov zakon gravitacije. Prema tom zakonu svaka čestica materije privlači svaku drugu česticu materije silom (F) koja je razmjerna umnošku njihovih masa, a obrnuto razmjerna kvadratu njihovih udaljenosti i usmjerena prema njihovoj spojnici. To je bio temelj Newtonove ili klasične teorije gravitacije, koju su dalje matematički razradili Siméon Denis Poisson, Pierre-Simon Laplace, Joseph-Louis Lagrange i Jean le Rond d'Alembert.
U nebeskoj mehanici dovoljno je pretpostaviti da su nebeska tijela materijalne točke, koje prema veličini svojih masa uzajamno djeluju jedna na drugu. Međutim, može se dokazati, a to je već i Newton učinio, da svaka kuglasta homogena masa, ili masa sastavljena od homogenih koncentričnih slojeva, djeluje na bilo koje drugo tijelo istom silom kojom bi djelovala da je sva njezina masa koncentrirana u središtu kugle. Tako se dobiva da je sila kojom Zemlja privlači neko tijelo mase m jednaka F = m ∙ g, gdje je m masa tog tijela, a g ubrzanje sile teže:
gdje je:
- G - univerzalna gravitacijska konstanta koja otprilike iznosi 6,67428 × 10−11 N m2 kg−2,
- M - masa Zemlje (kg),
- m - masa tijela na Zemlji (kg), i
- r0 - polumjer Zemlje (m).
U nebeskoj mehanici dovoljno je pretpostaviti da su nebeska tijela materijalne točke, koje prema veličini svojih masa uzajamno djeluju jedna na drugu. Međutim, može se dokazati, a to je već i Newton učinio, da svaka kuglasta homogena masa, ili masa sastavljena od homogenih koncentričnih slojeva, djeluje na bilo koje drugo tijelo istom silom kojom bi djelovala da je sva njezina masa koncentrirana u središtu kugle. Tako se dobiva da je sila F kojom Zemlja privlači neko fizikalno tijelo jednaka F = m∙g, gdje je m masa tog tijela, a g gravitacijsko ubrzanje:
ili ako se krati m s lijeve i desne strane jednadžbe:
U ovom obliku prepoznaje se Galileijev zakon, a Newtonova je zasluga što je dokazao da taj isti zakon vrijedi i za gibanje Mjeseca oko Zemlje te za gibanje planeta oko Sunca. Zbog rotacije, Zemlja je poprimila oblik geoida, to jest nije savršena kugla, nego je sploštena na polovima i izdužena na ekvatoru. Zbog rotacije i takva oblika Zemlje težina nekog tijela na polovima je oko 0,5% veća od njegove težine na ekvatoru. Raspored masa na površini Zemlje (oceana, planina), sastav Zemljine kore, visina od morske površine, i tako dalje, zajedno s rotacijom i sploštenošću Zemlje, uzrokuju da gravitacijsko ubrzanje varira od jedne do druge točke na Zemlji. Prihvaćena vrijednost za g0, gravitacijsko ubrzanje na morskoj površini, iznosi 9,80665 m/s2.[1]
Težina je sila koja djeluje na tijelo u gravitacijskom polju. Prema definiciji jakosti gravitacijskog polja težina je jednaka umnošku mase tijela m i jakosti gravitacijskog polja, to jest ubrzanja sile teže g:
Kako je težina sila, mjerna jedinica je, kao i za sve sile, njutn (N). Obično se težinu vrlo često zamjenjuje s masom, ali je to, gledajući fizikalno, potpuno pogrešno.[2]
Ako se tijelo nađe u sustavu koji se ubrzano giba, njegova će se težina promijeniti, primjerice težina se tijela u dizalu koje ubrzava prema dolje smanjuje, a u dizalu koje ubrzava prema gore povećava. U umjetnome satelitu koji kruži oko Zemlje, gravitacijsko se ubrzanje može poništiti centrifugalnim ubrzanjem, koje je suprotnoga smjera pa je onda težina jednaka nuli.
Slobodni pad je gibanje tijela isključivo pod utjecajem sile teže. Zakonitosti slobodnoga pada prvi je proučavao Galileo Galilei, te ustanovio da je prijeđeni put s proporcionalan kvadratu protekloga vremena t, a brzina v jednoliko raste s proteklim vremenom, te da gibanje ne ovisi o masi tijela koje pada. Na temelju Newtonovih jednadžbi gibanja i teorije gravitacije te se proporcionalnosti izražavaju jednadžbama:
gdje je: g - ubrzanje sile teže koje na Zemlji iznosi prosječno 9,80665 m/s² i mijenja se ovisno o položaju na površini Zemlje zbog njezina oblika (geoid), vrtnje (centrifugalna sila) i rasporeda mase (kopno–more). Na Mjesecu je površinsko gravitacijsko ubrzanje oko šest puta manje, a na Marsu tri puta. Te jednadžbe ne uzimaju u obzir otpor zraka pa striktno vrijede samo za slobodni pad u vakuumu, na primjer u vakumiranoj cijevi ili na svemirskim letjelicama bez atmosfere. Iz navedenih jednadžbi moguće je uklanjanjem veličine t dobiti treću jednadžbu za slobodni pad:
koja daje vrijednost brzine u pojedinim točkama prijeđenoga puta.[3]
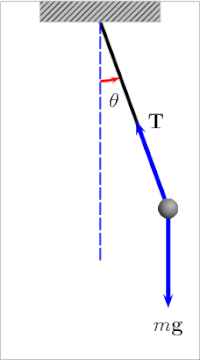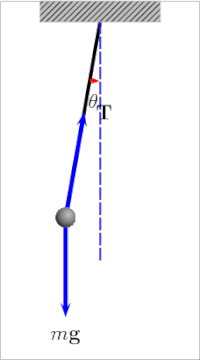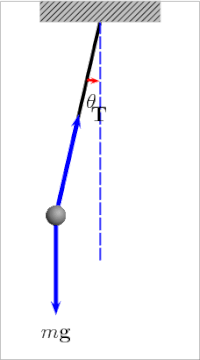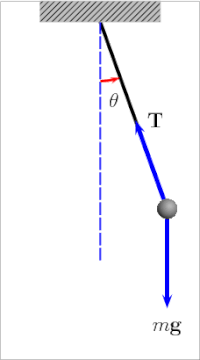
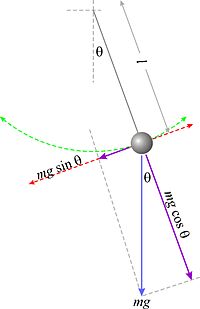
Pričvrstimo li malu olovnu kuglicu na tanku nit i otklonimo je za izvjestan kut od njenog ravnotežnog položaja, onda ta kuglica na niti vrlo male težine predstavlja matematičko njihalo. Kuglica se neće zaustaviti u svom ravnotežnom položaju već će oko njega titrati ili oscilirati. Put njihala između krajnjih točaka zove se jedan titraj, a vrijeme koje je potrebno da njihalo učini jedan titraj zove se period ili vrijeme titraja. Kod titranja njihala vrši se stalno pretvaranje potencijalne energije u kinetičku energiju i obratno. Kad njihalo podignemo iz položaja mirovanja na neku visinu h, dali smo mu izvjesnu potencijalnu energiju. Kinetička energija je u tom položaju jednaka nuli jer njihalo nema brzine. Kad njihalo pustimo, ono će se pod utjecajem komponente m∙g∙sin θ gibati, pa će njegova potencijalna energija opadati, a kinetička rasti. U najdonjem položaju (ravnotežnom položaju) bit će potencijalna energija jednaka nuli, dok će kinetička energija biti najveća jer je tu brzina najveća. Zbog tromosti ili inercije njihalo će produžiti svoje njihanje, te će ponovno kinetička energija opadati, a potencijalna rasti, a u krajnjoj točki ponovno će kinetička energija biti nula, a potencijalna najveća.
Kad ne bi bilo trenja u osloncu i otpora zraka, njihalo bi se stalno njihalo i uvijek bi se popelo do iste visine. Međutim, njegova se energija polagano troši na otpor zraka i trenje, te titraji postaju sve slabiji, dok se njihalo konačno ne umiri u ravnotežnoj točki. Sila koja prouzrokuje njihanje je:
Može se izračunati da je vrijeme jednog titraja:
a vrijeme jednog njihaja koji je polovina jednog titraja:
Iz ovog izraza proizlazi da trajanje jednog titraja ovisi o dvije veličine, o duljini njihala l i o ubrzanju g sile teže. Prema tome je trajanje jednog titraja:
- razmjerno (proporcionalno) s drugim korijenom iz duljine njihala l uz stalno g, to jest što je njihalo dulje, to je i vrijeme njihala veće, te se njihalo njiše polaganije. Što je njihalo kraće, vrijeme titraja je manje i njihalo se njiše brže;
- obrnuto razmjerno s ubrzanjem sile teže g uz konstantno l, to jest gdje je ubrzanje sile teže veće, tamo je vrijeme titraja kraće. Gdje je ubrzanje sile teže manje, tamo je i vrijeme titraja veće.
Trajanje jednog titraja ne ovisi:
- o težini, to jest o tome da li je njihalo lakše ili teže, da li je građeno od željeza, drva, olova ili bilo kojeg drugog materijala;
- o amplitudi. To znači da je vrijeme jednog titraja isto, bez obzira da li njihalo skrenemo iz položaja ravnoteže za veći ili manji kut. Praktički to vrijedi samo za male kutove približno do θ = 5°.[4]
- ↑ "Tehnička enciklopedija", glavni urednik Hrvoje Požar, Grafički zavod Hrvatske, 1987.
- ↑ težina, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2016.
- ↑ slobodni pad, [2] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
- ↑ Velimir Kruz: "Tehnička fizika za tehničke škole", "Školska knjiga" Zagreb, 1969.










