Tok polja

Tok vektorskog polja F kroz plohu S.

U matematici i fizici tok vektorskog polja je jedna od najreprezentativnijih veličina za vektorsko polje. Pojam potječe iz mehanike fluida u kojoj se za polje uzima polje brzina fluida, pa tok predočava količinu fluida proteklog u određenom vremenu kroz zamišljenu plohu u njegovoj struji. Veličina se često koristi i u drugim područjima fizike poput termodinamike, gdje može predstavljati tok toplinske struje ovisne o gradijentu polja temperatura, ili elektrodinamike, u kojoj se dva osnovna zakona u Maxwellovim jednadžbama mogu prikazati kao tok električnog ili magnetskog polja kroz zatvorenu plohu.

Definicija

Tok fluida brzine ${\vec {v}}$ kroz infinitezimalnu plohu površine $\mathrm {d} S$.

Ako se malena površina $\mathrm {d} S$ nalazi u struji fluida tako da njena normala ${\vec {n}}$ zatvara kut φ s vektorom lokalne brzine fluida ${\vec {v}}$, tada se sve čestice koje su početno bile na elementu površine $\mathrm {d} S$ pomaknu u smjeru vektora brzine za iznos koji je razmjeran brzini i vremenu protjecanja $\Delta t$, a obujam fluida koji je protekao tom površinom jednak je obujmu $\Delta V$ paralelepipeda kojem je osnovica $\mathrm {d} S$, a visina $v\,\Delta t\cos \varphi$. Vrijedi dakle $\Delta V=v\,\Delta t\cos \varphi \,\mathrm {d} S$. Tok polja ${\vec {v}}$ kroz element površine $\mathrm {d} S$ definira se kao brzina protoka volumena fluida, što odgovara jakosti struje, $\mathrm {d} \Phi =\Delta V/\Delta t$ pa je

$\mathrm {d} \Phi =v\cos \varphi \,dS$.

Budući da je $v\cos \varphi ={\vec {v}}\cdot {\vec {n}}$ (skalarni umnožak vektora) te da možemo definirati ${\vec {n}}\,\mathrm {d} S=\mathrm {d} {\vec {S}}$, slijedi

$\mathrm {d} \Phi ={\vec {v}}\cdot {\vec {n}}\,\mathrm {d} S={\vec {v}}\cdot \mathrm {d} {\vec {S}}.$

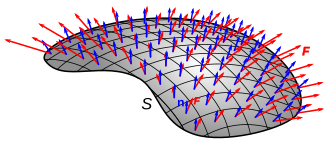
Tok polja ${\vec {v}}$ kroz cijelu površinu $S$ se prema tome definira kao zbroj infinitezimalnih doprinosa po elementima površine $\mathrm {d} S$, to jest kao integral

$\Phi {\stackrel {def.}{=}}\int \limits _{S}{\vec {v}}\cdot \mathrm {d} {\vec {S}}$.

I općenito, tok bilo kojeg vektorskog polja $\mathbf {F}$ kroz plohu $S$ je

$\Phi {\stackrel {def.}{=}}\int _{S}\mathbf {F} \cdot \mathrm {d} \mathbf {S}$.

Svojstva

Ako je površina zatvorena, tok fluida postaje plošni integral po zatvorenoj plohi

$\Phi =\oint _{S}{\vec {v}}\cdot \mathrm {d} {\vec {S}}.$

Ako je vektor ${\vec {v}}$ posvuda po plohi isti, tok je

$\Phi =\oint _{S}{\vec {v}}\cdot \mathrm {d} {\vec {S}}={\vec {v}}\oint _{S}\mathrm {d} {\vec {S}}=0$

jer je integral vektora zatvorene plohe jednak nuli. To pak znači da je u svakom trenutku količina fluida koji ulazi u zatvorenu plohu jednaka količini fluida koji iz nje izlazi. Ovo je uvijek slučaj za nestlačive fluide.

Općenito, ako unutar zatvorene plohe u vektorskom polju postoje izvori ili ponori polja, tok će biti različit od nule. U elektromagnetizmu, pozitivni naboji obuhvaćeni plohom doprinose toku električnoga polja iz plohe, a negativni naboji toku polja u plohu. Tok magnetskoga polja kroz zatvorenu plohu je pak uvijek nula, čime se izražava činjenica da ne postoje magnetski monopoli.

Kada polje treba lokalno opisati pomoću toka, koristi se mjera lokalne gustoće toka, dakle toka kroz malenu zatvorenu plohu u nekoj točki prostora podijeljenog obujmom plohe. Za to se definira divergencija vektorskog polja, $\mathrm {div} \mathbf {F}$ koja prema teoremu Gaussa i Ostrogradskog ima svojstvo da je njen volumni integral po unutrašnjosti plohe jednak toku polja kroz plohu,

$\oint _{V_{S}}\mathrm {div} \mathbf {F} \,\mathrm {d} V=\oint _{S}\mathbf {F} \cdot \mathrm {d} \mathbf {S}$.

Vezani pojmovi

• Vektorsko polje
• Gradijent skalarnog polja
• Rotacija vektorskog polja
• Vektorske operacije u zakrivljenim koordinatama