Težište






Težište je materijalna točka u kojoj djeluje rezultanta sila što djeluju na neko tijelo ili sustav materijalnih točaka u polju sile teže; u toj točki može se zamisliti kao da je sabrana sva masa tijela, odnosno sustava materijalnih točaka. Ako kruto tijelo ima središte, os ili ravninu simetrije, njegovo se težište podudara s tim središtem ili leži na toj osi, odnosno u toj ravnini. U praksi se težište krutoga tijela određuje tako da se tijelo objesi u nekoj od svojih točaka; tada, u položaju ravnoteže, težište tijela leži na okomici ispod objesišta. Ako se to isto ponovi u nekoj drugoj točki tijela, težište će ponovno ležati na okomici ispod objesišta. Sjecište tako određenih okomica bit će težište tijela. Ako se tijelo ili sustav materijalnih točaka ne nalazi u polju sile teže, određuje se na sličan način središte mase, što je općenitiji pojam od težišta.[1] Središte mase podudara se s težištem tijela ako je gravitacijsko ubrzanje konstantno i jednako u svim točkama tijela.[2] Pravac u kojem djeluje težina tijela, a prolazi kroz njegovo težište, zove se težišnica. Tijelo, poduprto u težištu, nalazi se u ravnoteži. Težište tijela ne mora se nalaziti u samom tijelu, ono može biti i izvan tijela, na primjer kod prstena.[3]
Težište materijalnog tijela[uredi | uredi kôd]
Težište materijalnog tijela je točka u kojoj kao da je sadržana sva težina tijela". Iako se ne može smatrati preciznom formalnom definicijom, ovaj opis otkriva smisao pojma težišta, koji se najčešće odnosi na ostvarivanje statičke ravnoteže u gravitacijskom polju. Mogući slučajevi općenito su poznati iz svakodnevnih primjena: materijalno tijelo obješeno iznad težišta nalazi se u stabilnoj ravnoteži (ako ga malo zakrenemo, nastoji se vratiti u prvobitni položaj); tijelo obješeno (poduprto) ispod težišta nalazi se u labilnoj ravnoteži (miruje točno u tome položaju; no ako ga imalo zakrenemo, prevrće se); tijelo obješeno u težištu nalazi se u indiferentnoj ravnoteži (može mirovati u tome položaju, ali i u bilo kojem drugom položaju u koji ga dovedemo zakretanjem oko težišta).
Pojam težište u površnim se tekstovima često brka s pojmom centar masa, jer se njihovi položaji kod manjih tijela na površini Zemlje tek neznatno razlikuju. U takvim slučajevima obično se za oba pojma koristi naziv težište, jer je taj pojam bliži svakodnevnom iskustvu i poznat još od antičkih vremena, dok se potreba za centrom masa javila tek u primjeni Newtonovih zakona gibanja. No, u ozbiljnijim udžbenicima definicije tih dvaju pojmova jasno su razgraničene.[4][5]
Precizna matematički formulirana definicija određuje težište materijalnog tijela kao hvatište njegove ukupne težine, tj. kao hvatište rezultantne sile koja zamjenjuje težine svih negovih dijelova (npr. težine svih čestica od kojih se tijelo sastoji). Hvatište rezultante nekog sustava sila određuje se pomoću momenata tih sila. Rezultanta, ako postoji, nije samo vektorski zbroj sila, nego ima takvo hvatište da je i njezin moment jednak zbroju njihovih momenata.
Iz toga proizlazi da položaj težišta materijalnog tijela nije određen samo građom tijela, nego ovisi i o obliku gravitacijskog polja u kojemu se tijelo nalazi. Zato općenito nisu uvijek ostvarivi svi spomenuti oblici statičke ravnoteže poznati iz iskustva u gravitacijskom polju na površini Zemlje. Za proizvoljni oblik gravitacijskog polja, položaj težišta ne mora biti jednoznačno određen (te u pravilu ovisi o orijentaciji tijela u polju), ili se uopće ne može odrediti - tj. tijelo uopće nema težišta (npr. u blizini točke gdje se gravitacijska polja Zemlje i Mjeseca dokidaju, može se tijelo orijentirati tako da težine njegovih dijelova čine spreg sila).
U ovome članku detaljnije se razmatra samo težište materijalnog tijela u gravitacijskom polju blizu površine Zemlje.
Usto, osim za materijalna tijela, uobičajeno je (u hrvatskom jeziku) pojam težišta definirati i kod nematerijalnih geometrijskih objekata (geometrijskih tijela, likova i linijia). U nekim drugim jezicima isti se pojam naziva centrom masa. Jasno je da je takva upotreba spomenutih termina metaforička, jer geometrijski objekti nemaju ni mase ni težine, ali je opravdana zbog analogija s homogenim materijalnim objektima. No, neki tekstovi umjesto toga koriste naziv centroid.
Računanje težišta materijalnog tijela[uredi | uredi kôd]
Težište materijalnog tijela je točka T koja je hvatište ukupne težine tijela (rezultante težina svih čestica od kojih se tijelo sastoji). Za tijelo od N čestica ta točka T, opisana vektorom položaja , mora zadovoljiti jednadžbu koja zahtijeva da moment ukupne težine bude jednak zbroju momenata težina pojedinih čestica:
- (gdje je ukupna težina tijela).
Pojedina čestica označena je simbolom "i" (i=1, 2, ... N). Njezina masa je , njezin vektor položaja je , a njezina težina računa se kao umnožak njezine mase i gravitacijskog polja na mjestu gdje se čestica nalazi.
Iz same jednadžbe nije unaprijed jasno da li je uopće moguće odrediti makar jednu točku T za koju će jednadžba biti zadovoljena, jer to ovisi o gravitacijskom polju i rasporedu mase tijela u njemu. A ako za neku orijentaciju tijela u polju i postoji takva točka (u koju se može postaviti hvatište rezultantne težine), ona nije jednoznačno određena gornjom jednadžbom, jer će i svaka druga točka na pravcu rezultante zadovoljiti tu jednadžbu za istu orijentaciju tijela. No, tada se mogućnost jednoznačnog definiranja težišta ispituje tako da se varira orijentacija tijela u polju. Pritom se promatra i da li je moguće ostvariti različite oblike statičke ravnoteže vezane uz težište (labilnu, stabilnu, indiferentnu).
U stvarnom izračunu obično se, umjesto ogromnog broja diskretnih sastavnih čestica, zamišlja kontinuirana razdioba tijela na sve sitnije dijelove, koji se graničnim procesom prevode u diferencijalne elemente mase , pa se sume iz gornje formule prevode u integrale, što omogućuje korištenje poznatih metoda diferencijalnog računa.
Ovdje se razmatra težište materijalnog tijela samo u homogenom gravitacijskom polju, te u približno homogenom polju blizu površine Zemlje.
Težište materijalnog tijela u homogenom gravitacijskom polju[uredi | uredi kôd]
U ogromnoj većini praktičnih primjena može se smatrati da je gravitacijsko polje u blizini Zemlje posve homogeno na malim udaljenostima, tj. da u svakoj točki promatranog tijela polje ima isti iznos i smjer. Uz tu pretpostavku, težište T materijalnog tijela nalazi se u istoj točki kao i centar masa tijela, pa se može računati npr. po formuli
- (gdje je ukupna masa sustava)
kao i po drugim formulama za određivanje centra masa tijela. Dokaz ove tvrdnje je jednostavan: u jednadžbi za momente treba samo zamijeniti različite vrijednosti gravitacijskog polja s konstantnim vektorom koji se može izlučiti iz sume tako da se dobije
Izraz u zagradi jednak je (prema definiciji centra masa) umnošku , i to za bilo koju orijentaciju tijela u polju, pa jednakost može biti ispunjena samo ako se težište nalazi u centru masa. Usto, nije teško pokazati da se za odgovarajuće točke ovjesa može postići stabilna, labilna i indiferentna ravnoteža.
U praktičnom računu, gornja vektorska jednadžba za vektor položaja težišta razlaže se na skalarne komponente, pa se zasebno računaju pojedine koordinate težišta. Pritom se obično koristi formula u kojoj je sumiranje zamijenjeno integriranjem, a masa opisana preko gustoće - kao kod računanja centra masa. Isto tako, sumiranje se uglavnom koristi kada je tijelo sastavljeno od nekoliko dijelova kojima su poznati položaji težišta; tada se, na primjer, y-koordinata težišta za tijelo ukupne mase računa kao
gdje je masa pojedinog dijela tijela, a y-koordinata težišta toga dijela je .
Težište materijalnog tijela u stvarnom gravitacijskom polju blizu površine Zemlje[uredi | uredi kôd]
Stvarno Zemljino gravitacijsko polje nije homogeno: iznos mu opada s kvadratom udaljenosti od središta Zemlje, i usmjereno je prema središtu Zemlje. No, odstupanja od homogenosti vrlo su mala na manjim udaljenostima: blizu površine Zemlje jakost polja umanjuje se samo za oko 0,03% po jednom kilometru vertikalnog uspona, a smjerovi polja na horizontalnoj udaljenosti od 1 km zatvaraju kut od samo 0,009 stupnjeva. Zato se za objekte manjih dimenzija (nekoliko metara) može pretostaviti potpuna homogenost gravitacijskog polja, jer će npr. i neznatno trenje posve prikriti činjenicu da se položaj težišta može razlikovati od centra masa za koji djelić milimetra.
Međutim, razlika načelno postoji, te može imati izvjesnog značaja kod objekata većih dimenzija i kod preciznijih mjerenja. Za ilustraciju prikladno je razmotriti tanki štap (na skici desno), za koji će se radi jednostavnosti pretpostaviti da je homogen (ima posvuda jednaku gustoću). Kad je štap u vertikalnom položaju (os y pokazuje uvis) njegovo težište T nalazi se ispod centra masa C (dakle, bliže kraju A štapa). To se naslućuje čak i intuitivno, zato što je donja polovica štapa teža (jer je u jačem gravitacijskom polju od gornje). No, za precizno određivanje položaja težišta zgodno je zamisliti vrlo mali otklon štapa od vertikale. Ako ga objesimo u nekoj točki malo ispod C, težina donjega dijela nastoji ga vratiti u vertikalni položaj, dok ga težina gornjega dijela nastoji otkloniti još dalje. Težište mora biti u onoj točki za koju se momenti težina gornjeg i donjeg dijela štapa točno poništavaju (pa će štap biti u stabilnoj ravnoteži ako se objesi bilo gdje iznad težišta). Račun pokazuje da se T nalazi vrlo blizu C: ako bi štap bio dugačak 1 kilometar, težište bi bilo samo nekoliko centimetara ispod centra masa.
No, ako se promotri isti štap u horizontalnom položaju, jasno je da težište više ne može biti bliže kraju A štapa: zbog simetričnosti gravitacijskog polja, ono mora biti jednako udaljeno od oba kraja štapa. I ne samo da se težište pomaklo u odnosu na štap, nego u modelu tankoga štapa za taj položaj više nije moguće uspostaviti indiferentnu ili stabilnu ravnotežu.
Aproksimacija paralelnog polja[uredi | uredi kôd]
Budući da je blizu površine Zemlje odstupanje gravitacijskog polja od stroge paralelnosti manje značajno nego njegovo opadanje s visinom, neki autori[6] računaju (približni) položaj težišta na Zemlji pomoću prosječne visinske raspodjele težine uz pretpostavku da su težine svih čestica paralelne (pa se ne opisuju kao vektori, nego samo kao iznosi težina koji ovise o visini):
- (gdje je ukupni iznos težine sustava).
Za tanki homogeni štap u verikalnom položaju (iz gornjeg primjera) na ovaj se način dobije isti položaj težišta kao uravnoteživanjem momenata za infinitezimalni otklon od vertikale.
Težište kao izvor gravitacijskog polja[uredi | uredi kôd]
U engleskom jeziku za težište se koristi termin "centar gravitacije" (center of gravity). Sukladno takvom nazivu, težište ne mora označavati samo "točku u kojoj kao da je sadržana sva težina tijela koje se nalazi u vanjskom gravitacijskom polju", nego alternativno može označavati i "točku u kojoj kao da se nalazi izvor gravitacijskog polja koje tijelo proizvodi".
Ta točka (težište kao izvor polja) općenito ovisi o položaju promatrača (osim za sferno simetrična tijela). No, za pojedinog promatrača čiji je položaj određen vektorom , težište kao izvor polja koje potječe od nekog tijela ili sustava čestica ukupne mase M jednoznačno je određeno izrazom[7]:
Težište geometrijskog objekta[uredi | uredi kôd]
Težište geometrijskog tijela, lika ili linije je točka koja se označava simbolom T ili C (naziva se još i centar masa ili centroid), a računa se na isti način kao i centar masa homogenog materijalnog tijela:
- (za tijelo); (za lik); (za liniju).
Integriranje po volumenu, plohi i liniji naznačeno je samo simbolički (slovima V, A te l).
Naziv "težište" za geometrijske objekte opravdan je zbog analogije s težištem homogenih materijalnih objekata u homogenom gravitacijskom polju: kod težišta geometrijskog tijela može se zamišljati da se radi o homogenom materijalnom tijelu, kod ravninskog lika analogija je tanka homogena ploča, kod ravne linije tanki homogeni štap itd.
Neovisno o tim analogijama, težište geometrijskog objekta, kao matematički pojam, ima različite primjene u matematici. Jedna od najpoznatijih primjena je računanje volumena rotacionih tijela i površine rotacionih ploha pomoću Pappus-Guldinovih pravila.
Osim primjena u matematici, težišta geometrijskih objekata često se računaju i koriste u tehničkoj mehanici, osobito kod elemenata konstrukcija.[8]
Određivanje težišta geometrijskih objekata znatno je jednostavnije kod simetričnih objekata, jer se težište nalazi na simetrali, pa se u najjednostavnijim slučajevima može odrediti kao presjecište simetrala. U dolje prikazanim primjerima većina objekata ima jednu os simetrije, duž koje je postavljena koordinatna os y na kojoj leži težište, a računa se samo y-koordinata težišta.
Često se geometrijski objekt sastoji od nekoliko dijelova kojima su poznati položaji njihovih težišta. Tada nije potrebno težište određivati integriranjem, nego se koristi jednostavno sumiranje po tim dijelovima. Primjerice, y-koordinata težišta ravninskog lika ukupne površine A računa se po formuli
gdje je površina pojedinog dijela, a y-koordinata njegovog težišta je .
Primjeri težišta nekih geometrijskih objekata[uredi | uredi kôd]
Ovdje se opisuje položaj težišta za neke često korištene linije, plohe i geometrijska tijela.
Težišta linija[uredi | uredi kôd]

- Dužina
- Težište je na polovici dužine.
- Kružni luk s polumjerom r i kutom
gdje je polovica kuta sadržanoga ispod kružnog luka, a "kapa" nad simbolom označava da kut treba računati u radijanima.
Težišta geometrijskih likova[uredi | uredi kôd]
- Paralelogram
- Težište je na presjeku dijagonala.
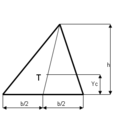
- Trokut
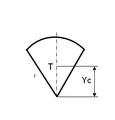
- Kružni isječak
gdje je polovica kuta sadržanoga ispod kružnog luka, a "kapa" nad simbolom označava da kut treba računati u radijanima.
- Kružni odsječak
gdje je polovica kuta sadržanoga ispod kružnog luka, a "kapa" nad simbolom označava da kut treba računati u radijanima.
-
Trokut
-
Kružni isječak
-
Kružni odsječak
Težišta geometrijskih tijela[uredi | uredi kôd]
- Kocka, prizma, kugla
- Težište je u središtu.
- Piramida i stožac
- Polukugla
- Kalota (kuglin odsječak)
- Kuglin isječak
-
Piramida ili stožac
-
Polukugla
-
Kalota
-
Kuglin isječak
Primjer određivanja težišta složenog tijela[uredi | uredi kôd]

Umjesto gornjih formula za težišta, u kojima se koristi vektor položaja kao oznaka za sve tri koordinate centra masa, u praktičnim se primjenama najčešće pojedina kooordinata zasebno računa. Tako na primjer u Kartezijevom sustavu za x-koordinatu centra masa sustava od N čestica imamo (a i preostale dvije koordinate, ako je potrebno, računaju se iz analognih izraza):
- .

Račun prikazujemo na jednostavnom primjeru: na skici desno prikazan je čekić kojemu se težište nalazi na osi x zbog simetričnog rasporeda masa. Na početnom dijelu osi naznačene su jedinice duljine (na primjer centimetri): glava čekića mase m1=2kg ima težište u svojemu središtu, na koordinati x1=2cm, a drška mase m2=0,5kg na koordinati x2=6 cm.
Težište tijela s ovako opisanim dijelovima računa se (kako je već spomenuto) po jednakosti za težište sustava čestica, pa imamo:
Baricentar[uredi | uredi kôd]
Baricentar (grč. bari- ili βαρύ-ς: teško + centar: središte), težište ili središte mase, u astronomiji je točka oko koje se gibaju nebeska tijela dvojnog ili višestrukog sustava. Baricentar sustava Zemlje i Mjeseca nalazi se unutar Zemljine površine na udaljenosti 4670 kilometara od središta (oko 74% Zemljinog polumjera). Ta se točka sustava, a ne središte Zemlje, giba po eliptičnoj stazi oko Sunca.[9]
Izvori[uredi | uredi kôd]
- ↑ težište, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
- ↑ središte mase, [2] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
- ↑ Velimir Kruz: "Tehnička fizika za tehničke škole", "Školska knjiga" Zagreb, 1969.
- ↑ Young H. D., Freedman R. A., Sears and Zemansky University Physics, Addison-Wesley, San Francisco (2004)
- ↑ Richard Feynman, The Feynman Lectures on Physics; Volume 1, Addison-Wesley, U.S.A (1964)
- ↑ Beatty, Millard F., Principles of Engineering Mechanics, Volume 2: Dynamics—The Analysis of Motion, Springer, Mathematical Concepts and Methods in Science and Engineering (2006)
- ↑ Symon, Keith R., Mechanics, Addison-Wesley (1964)
- ↑ Josip Brnić, Mehanika i elementi konstrukcija, Školska knjiga, Zagreb (1993)
- ↑ baricentar, [3] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2014.