Zemljina rotacija
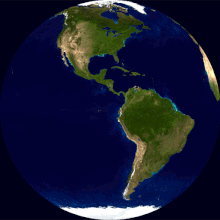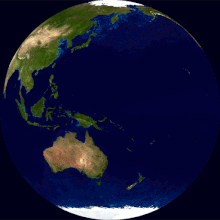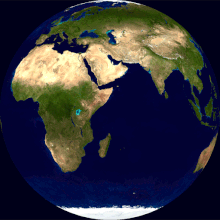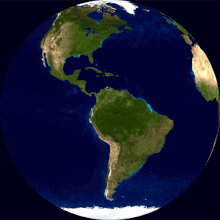
Zemljina rotacija je rotacija krutog tijela Zemlje oko svoje osi. Zemlja se rotira prema istoku. Gledajući sa Sjeverne Zvijezde Polaris, Zemlja se vrti suprotno od kazaljke na satu.

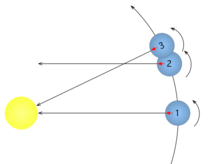
Period rotacije Zemlje u relativnom odnosu na Sunce (od pravog podneva do pravog podneva) je njen pravi sunčev dan ili sinodički dan. On ovisi o kretanju Zemlje po orbiti i zbog toga na njega utječu promjene u ekscentricitetu i nagibu Zemljine orbite. Oba variraju kroz tisuće godina[1] tako da i godišnje varijacije pravog sunčevog dana također variraju. Generalno, pravi sunčev dan dulji je od srednjeg sunčevog dana između dva perioda godine i kraći između sljedeća dva. Pravi sunčev dan sklon je da bude dulji blizu perihela kada se sunce prividno kreće duž ekliptike pod većim kutom nego inače, kada mu treba oko 10 sekundi dulje. Suprotno tome, oko 10 sekundi je kraći blizu afea. Oko 20 sekundi je duži blizu solsticija kada projekcija prividnog gibanja Sunca duž ekliptika na nebeski ekvator uzrokuje Sunce da se kreće pod većim kutom nego inače. Suprotno tome, blizu ekvinoksa projekcija na ekvator je kraća za oko 20 sekundi. Trenutno, efekti perifeliona i solsticija se kombiniraju da bi produljili pravi sunčev dan blizu 22. prosinca za 30 srednjih sunčevih sekundi, ali efekt solsticija je djelomično poništen efektom apheliona oko 19. lipnja kada je samo 13 sekundi duži. Efekti ekvinoksa skraćuju ga oko 26. ožujka i 16. rujna za 18, odnosno 21 sekundu.[2][3][4]
Prosječno trajanje pravog sunčevog dana kroz cijelu godinu je srednji sunčev dan, koji traje 86,400 srednjih sunčevih sekundi. Trenutno, svaka ova sekudna je malo dulja od SI sekunde zato što je Zemljin srednji sunčev dan sada malo dulji nego što je bio tijekom 19. stoljeća zbog efekta plime i oseke. Prosječna duljina srednjeg sunčevog dana od uvođenja preskočne sekunde 1972. godine je oko 0 do 2 ms veća od 86,400 SI sekunde. [5][6][7] Nasumične fluktuacije zbog odnosa između jezgre i plašta Zemlje imaju amplitudu od oko 5ms. [8][9] Srednju sunčevu sekundu između 1750. i 1892. godine odabrao je 1895. godine Simon Newcomb kao neovisnu jedinicu vremena u svojim Tablicama Sunca. Ove tablice su korištene za izračune zemljinih efemerida između 1900. i 1983. godine, pa je ova sekunda postala poznata kao efemerijska sekunda. SI sekunda izjednačena je s efemerijskom sekudnom 1967. godine.[10]
Pravo sunčevo vrijeme je mjera rotacije Zemlje i razlika između te mjere i srednjeg sunčevog vremena je poznata kao jednadžba vremena.
Period rotacije Zemlje ovisno o fiksnim zvijezdama, nazvan zvjezdani dan od IERS, je 86,164.098 903 691 sekunde srednjeg sunčevog vremena (UT1) (23h 56m 4.098 903 691s, 0.997 269 663 237 16 srednjeg sunčevog dana). [11][n 1] Period rotacije Zemlje ovisno o precesijskoj ili pomičnoj proljetnoj ravnodnevnici nazvan je siderički dan,[n 2] kojem je trajanje 86 164,090 530 832 88 sekundi srednjeg sunčevog vremena (UT1) (23h 56m 4,090 530 832 88s, 0,997 269 566 329 08 srednjeg sunčevog dana).[11] Tako je siderički dan kraći od zvjezdanog dana za oko 8.4 ms. .[13] 499. godine Arybhata, veliki matematičar-astronom iz klasičnog doba indijske matematike i indijske astronomiije procijenio je duljinu sideričkog dana kao 23h 56m 4.1s.[14]
I zvjezdani dan i siderički dan su kraći od srednjeg sunčevog dana za oko 3 minute i 56 sekundi. Srednji sunčev dan u SI sekundama dostupan je kod IERS-a za periode od 1623-2005.[15] i 1962-2005. godine.[16]

Nedavno (1999. – 2010.) prosječno godišnje trajanje srednjeg sunčevog dana u odnosu na 86,400 SI sekundi variralo je između 0.25 i 1 ms, što mora biti dodano i zvjezdanim i sideričkim danima danim u srednjem sunčevom vremenu prikazanom gore da bi se dobila njihova trajanja u SI sekundama.
Kutna brzina rotacije Zemlje u inercijskom prostoru je (7.2921150 ± 0.0000001) ×10'-5' radijana po SI sekundi (srednja sunčeva sekunda).[11] Množeći sa (180°/Π radijana)x(86,400 sekundi/srednjeg sunčevog dana) daje 360.9856°/srednjem sunčevom danu, ukazujući da se Zemlja rotira više od 360° u odnosu na fiksne zvijezde u jednom sunčevom danu. Kretanje Zemlje po svojoj približno kružnoj orbiti dok se rotira jedanput oko svoje osi zahtjeva da se Zemlja zarotira malo više nego jednom u odnosu na fiksne zvijezde prije nego nam srednje Sunce može proći iznad glave opet, iako se rotira samo jednom (360°) u odnosu na Sunce.[n 3] Množeći vrijednost u rad/s s radijusom ekvatora Zemlje od 6,378,137 m (WGS84 elipsoid) (faktori od 2Π radijana od oba se poništavaju) izručuje brzinu na ekvatoru od 465.1 m/s ili 1674.4 km/h.[17] Neki izvori izjašnjavaju da je brzina rotacije Zemlje na ekvatoru nešto manja, oko 1669.8 km/h.[18] To je dobiveno dijeljenjem Zemljinog opsega na ekvatoru s 24 sata. Premda, korištenje samo jednog opsega implicira samo jednu rotaciju u inercijskom prostoru, pa odgovarajuća vremenska jedinica mora biti siderički sat. To je potrvrđeno množenjem broja sideričkih dana u jednom srednjem sunčevom danu, 1.002 737 909 350 795,[11] što rezultira brzinu na ekvatoru u srednjim sunčevim satima danu iznad od 1674.4 km/h.
Kutna brzina rotacije Zemlje na nekoj točki može se pretpostaviti množenjem brzine na ekvatoru s kosinusom širine.[19] Na primjer, Kennedy Space Centar je smješten na 28.59° sjeverne širine što daje brzinu od 1,674 km/hr * cos (28.59) = 1,470.23 km/h.
Stalno praćenje rotacije Zemlje zahtjeva uporabu Very Long Baseline Interferometry]] u koordinaciji s GPS-om, Satellite laser ranging i ostalim satelitskim tehnikama. Ovo omogućava apsolutne podatke za određivanje univerzalnog vremena, precesije, i nutacije.[20]
Kroz milijune godina, rotacija se značajno usporila zbog gravitacijske interakcije s Mjesecom: vidi akceleracija plime i oseke. Premda su neki veliki događaji, kao potres u Indijskom Oceanu 2004. godine, prouzročili da se brzina rotacije poveća za 3 mikrosekunde.[21] Post-glacijalni udar, koji traje od posljednjeg ledenog doba, mijenja raspored Zemljine mase i tako utječe na Moment inercije Zemlje i, po zakonu očuvanja količine gibanja, na period rotacije Zemlje.[22]
Os Zemljine rotacije kreće se u odnosu na fiksne zvijezde (inercijski prostor); komponente ove kretnje su precesija i nutacija. Os Zemljine rotacije također se kreće u odnosu na Zemljinu koru, što se zove polarno kretanje.
Precesija je rotacija osi Zemljine rotacije, uzrokovana uglavnom vanjskim okretnim momentom od gravitacije Sunca, Mjeseca i ostalih tijela. Polarno kretanje dešava se prvenstveno zbog uvrtanja (nutacije) slobodne jezgre i Chandlerovog njihanja.
Brzina rotacije Zemlje imala je različite utjecaje tokom vremena, ukljućujući i oblik same Zemlje (geoid), klimu, dubine i struje oceana, te tektonske sile.[23]

Teoretizira se o tome da se Zemlja formirala kao dio rođenja Sunčevog sustava: ono što je eventualno postalo sunčev sustav u početku je postojalo kao veliki, rotirajući oblak prašine, kamenja, i plina. Taj oblak bio je sastavljen od vodika i helija nastalih iz velikog praska, kao i od težih elemenata izbačenih supernovama. Kako je taj međuzvjezdani prah bio nehomogen, svaka asimetrija tokom gravitacijskih djelovanja rezultirala je okretnim momentom eventualnog planeta.[24] Sadašnji period rotacije zemlje rezultat je te početne rotacije i ostalih faktora, koji uključuju akceleraciju plime i oseke i hipotetski udar asteroida Theia
U rotacijskom referentnom okviru Zemlje, slobodno krećuće tijelo prati prividni put koji odskače od onoga koje bi pratilo da se nalazi u fiksnom referentnom okviru. Zbog tog Coriolisovog učinka, padajuća tijela skreću prema istoku od vertikalne linije viska ispod točke s koje su otpušteni. I projektili skreću desno na sjevernoj polutki (i lijevo na južnoj) od smjera u kojem su ispaljeni. Coriolisov učinak se manifestira na još načina, posebno u meteorologiji, gdje je odgovoran za mijenjanje smjera rotacije ciklona na sjevernoj i južnoj polutki. Hooke je, prateći Newtonov prijedlog iz 1679. godine, neuspješno pokušao potvrditi predviđenu devijaciju od pola milimetra prema istoku tijela bačenog s visine od 8.2 metra, ali prave rezultate su dobili tek kasnije pri kraju 18. i početku 19. stoljeća Giovanni Battista Guglielmini u Bologni, Johann Friedrich Benzenberg u Hamburgu i Ferdinand Reich u Freibergu, koristeći više tornjeve i pažljivo ispuštene utege.[n 4]
Najslavniji test i dokaz rotacije Zemlje je Foucaultovo njihalo kojeg je prvi izgradio fizičar Léon Foucault 1851. godine. Njihalo se sastojalo od 28 kg teške olovne jezgre obložene mjedom obješene sa 67 m visoke kupole Pantheona u Parizu. Zbog rotacije Zemlje pod njišućim njihalom ravnina oscilacije čini se da rotira ovisno zemljinoj širini. Na širini u Parizu predviđen i promatran pomak bio je oko 11 stupnjeva u smjeru kazaljke na satu po satu. Foucaultova njihala sada se njišu po muzejima po cijelom svijetu.
- ↑ Aoki, the ultimate source of these figures, uses the term "seconds of UT1" instead of "seconds of mean solar time".[12]
- ↑ Sidereal day is arguably a misnomer because the dictionary definition of sidereal is "relating to the stars", thus fostering confusion with the stellar day.
- ↑ In astronomy, unlike geometry, 360° means returning to the same point in some cyclical time scale, either one mean solar day or one sidereal day for rotation on Earth's axis, or one sidereal year or one mean tropical year or even one mean Julian year containing exactly 365.25 days for revolution around the Sun.
- ↑ See Fallexperimente zum Nachweis der Erdrotation (German Wikipedia article).
- ↑ Derivation of the equation of time. Inačica izvorne stranice arhivirana 24. rujna 2010. Pristupljeno 15. travnja 2011.
- ↑ Jean Meeus, Mathematical astronomy morsels (Richmond, Virginia: Willmann-Bell, 1997) 345–6.
- ↑ Equation of time in red and true solar day in blue
- ↑ The duration of the true solar day
- ↑ http://hpiers.obspm.fr/eoppc/eop/eopc04_05/eopc04.62-now
- ↑ Physical basis of leap seconds
- ↑ Leap seconds. Inačica izvorne stranice arhivirana 27. svibnja 2012. Pristupljeno 15. travnja 2011. journal zahtijeva
|journal=(pomoć) - ↑ Prediction of Universal Time and LOD Variations (PDF). Inačica izvorne stranice (PDF) arhivirana 28. veljače 2008. Pristupljeno 15. travnja 2011.
- ↑ R. Hide et al., "Topographic core-mantle coupling and fluctuations in the Earth's rotation" 1993.
- ↑ Leap seconds by USNO. Inačica izvorne stranice arhivirana 27. svibnja 2012. Pristupljeno 15. travnja 2011. journal zahtijeva
|journal=(pomoć) - ↑ a b c d IERS EOP Useful constants
- ↑ Aoki, et al., "The new definition of Universal Time", Astronomy and Astrophysics 105 (1982) 359–361.
- ↑ Explanatory Supplement to the Astronomical Almanac, ed. P. Kenneth Seidelmann, Mill Valley, Cal., University Science Books, 1992, p.48, ISBN 0-935702-68-7.
- ↑ Aryabhatiya Arhivirana inačica izvorne stranice od 15. kolovoza 2011. (Wayback Machine) आर्यभटीय, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.25, ISBN 978-81-7434-480-9
- ↑ IERS Excess of the duration of the day to 86,400s … since 1623 Arhivirana inačica izvorne stranice od 3. listopada 2008. (Wayback Machine) Graph at end.
- ↑ IERS Variations in the duration of the day 1962–2005
- ↑ Arthur N. Cox, ed., Allen's Astrophysical Quantities p.244.
- ↑ Michael E. Bakich, The Cambridge planetary handbook, p.50.
- ↑ Butterworth and Palmer. Speed of the turning of the Earth. Ask an Astrophysicist. NASA Goddard Spaceflight Center
- ↑ Permanent monitoring
- ↑ Sumatran earthquake sped up Earth's rotation, Nature, December 30, 2004.
- ↑ Wu, P.; Peltier, W.R. 1984. Pleistocene deglaciation and the earth's rotation: a new analysis. Geophysical Journal of the Royal Astronomical Society. 76: 753–792
- ↑ Physical effects. Inačica izvorne stranice arhivirana 8. listopada 2010. Pristupljeno 15. travnja 2011. journal zahtijeva
|journal=(pomoć) - ↑ Why do planets rotate?. Ask an Astronomer

