Moment inercije



Moment tromosti ili moment inercije (znak I ili J) je fizikalna veličina koja opisuje tromost ili inerciju čestice ili krutoga tijela pri promjeni brzine ili smjera vrtnje; jednaka je zbroju umnožaka mase m i kvadrata udaljenosti r od osi rotacije svake čestice koja čini tijelo:
Moment inercije je ustvari mjera tromosti za vrtnju ili rotacijsko gibanje. Može se reći da je moment inercije rotacijska analogija mase. Što je moment inercije nekog tijela veći to ga je teže pokrenuti u rotaciju ili zaustaviti njegovu rotaciju. Međutim, za razliku od mase, moment inercije nije neka nepromjenjiva veličina; on ovisi o osi oko koje se dešava rotacija tijela. Matematička definicija momenta inercije I materijalne točke mase m za neku os a je:
gdje je r udaljenost te točke od osi rotacije. Mjerna jedinica za moment inercije je kgm².
Za neko tijelo sastavljeno od N materijalnih čestica moment inercije za neku os je jednak zbroju momenata inercije svih materijalnih čestica za tu istu os:
Ovo je nepraktičan izraz za neko kontinuirano tijelo za koji bi trebalo znati točan broj i položaj svih čestica. Umjesto toga integriraju se momenti inercije svih diferencijalnih masa dm:
Uz pretpostavku da je gustoća tijela ρ po cijelom volumenu jednaka, dobivamo:
Momenti inercije za osi koje prolaze kroz težište tijela nazivaju se vlastitim momentima inercije. Iako gornja matematička formulacija vrijedi posve općenito, moment inercije za neku os koja prolazi izvan težišta tijela se može izračunati pomoću Steinerovog pravila koje možemo ovako sročiti:
- Moment inercije tijela za neku os koja ne prolazi težištem jednak je zbroju vlastitog momenta inercije za os paralelnu s traženom osi i umnoška mase tijela s kvadratom udaljenosti težišta tijela od tražene osi .
Ovo je pravilo vrlo važno i elementarno. Umnožak mase tijela i kvadrata udaljenosti težišta tijela od tražene osi se naziva položajni moment inercije.
Matematički izričaj Steinerovog pravila možemo zapisati na sljedeći način:
Iz svega izloženoga treba uočiti nekoliko činjenica bitnih za razumijevanje materije:
- Što je neka masa udaljenija od osi rotacije, to je teže vršiti rotaciju.
- Inertnost ili tromost mase pri rotaciji raste s kvadratom udaljenosti od osi rotacije.
- Materijalna točka nema vlastitih momenata inercije jer nema protežnost.
- Za dovoljno kompaktna tijela (na primjer mala kugla) u nekim slučajevima možemo aproksimirati da nemaju vlastitih momenata inercije.
- Moment inercije nekog tijela ne ovisi samo o negovoj masi i udaljenosti njegovog težišta od osi rotacije, već i o obliku.
- Steinerovo pravilo se primjenjuje bez obzira na to da li os rotacije prolazi kroz tijelo ili se nalazi izvan njega, bitan je samo odnos osi prema težištu.
Moment tromosti nekih tijela[uredi | uredi kôd]
Moment tromosti nekog tijela ovisi o obliku tijela, raspodjeli mase, položaju osi rotacije. Primjerice, ako je m masa tijela, r njegov polumjer, a os rotacije ujedno i os simetrije, moment inercije na primjer šupljega valjka ili prstena iznosi:
homogeno ispunjenoga valjka ili kružne ploče:
homogeno ispunjene kugle:
Moment tromosti homogeno ispunjenoga štapa kojemu je os rotacije okomita na dužinu štapa nalazi se na polovici dužine štapa l:
a na kraju je štapa:
gdje je: l - duljina štapa. Mjerna je jedinica momenta tromosti kilogram puta kvadratni metar (kg m2).[1]
Momenti tromosti nekih presjeka[uredi | uredi kôd]
| Opis | Slika | Moment tromosti | Primjedba | Literatura |
|---|---|---|---|---|
| puni kružni presjek (šipka) s polumjerom r |  |
[2] | ||
| prsten (cijev) s unutarnjim polumjerom r1 i vanjskim polumjerom r2 | 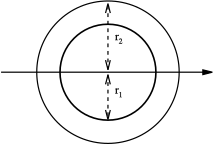 |
Za tanke cijevi, i .
Možemo reći da , i zbog ta zagrada se može pojednostaviti u . Konačno, za tankostijenu cijev proizlazi, . |
||
| puni kružni isječak s kutom θ u radijanima i polumjerom r, s obzirom na os kola prolazi kroz težište i središte kružnice |  |
Jednakost vrijedi samo za 0 ≤ ≤ | ||
| puni polukrug s polumjerom r u odnosu na vodoravni pravac koji prolazi kroz težište |  |
[3] | ||
| puni polukrug s polumjerom r u odnosu na vodoravni pravac koji prolazi kroz osnovu |  |
Udaljenost između težišta i osnove je | [3] | |
| puni polukrug s polumjerom r u odnosu na okomiti pravac koji prolazi kroz težište |  |
[3] | ||
| puna četvrtina kruga s polumjerom r s obzirom na središte kruga. |  |
[4] | ||
| puna četvrtina kruga s polumjerom r s obzirom na pravac prolazi kroz težište |  |
Udaljenost između težišta i baze je | [4] | |
| puna elipsa s poluosima a (uzduž osi x) i b |  | |||
| puni pravokutnik s osnovicom a i visinom h u odnosu na pravac koji prolazi kroz težište |  |
[5] | ||
| puni pravokutnik s osnovicom a i visinom h u odnosu na pravac koji prolazi kroz osnovicu |  |
[5] | ||
| puni trokut s osnovicom b i visinom h u odnosu na pravac koji prolazi kroz težište |  |
[6] | ||
| puni trokut s osnovicom b i visinom h u odnosu na pravac koji prolazi kroz osnovicu |  |
[6] | ||
| puni šesterokut sa stranicom a, pravac prolazi kroz težište ili središte |  |
Isto vrijedi i za okomiti pravac. |
Primjena[uredi | uredi kôd]
Savijanje[uredi | uredi kôd]



Savijanje ili fleksija (engl. bending, flexure) je opterećenje koje djeluje okomito na uzdužnu os nosača. Za razliku od osnog opterećenja (vlak i tlak), pri savijanju štapa deformira se uzdužna os štapa. Deformirana uzdužna os zove se elastična linija ili progib. Razlikuje se čisto savijanje i poprečno savijanje. Pri čistom savijanju sve su komponente unutrašnjih sila jednake nuli, osim momenta savijanja. Pri poprečnom savijanju osim momenta savijanja pojavljuje se još i poprečna sila koja uzrokuje smicanje. Čisto savijanje zove se još i savijanje spregovima, a poprečno savijanje, savijanje silama. Moment savijanja uzrokuje normalna naprezanja σ koja se zamišljaju razdijeljenima po presjeku razmjerno udaljenosti od neutralne osi. Neutralna os prolazi kroz težište promatranog presjeka. Klasična jednakost koja određuje naprezanje u gredi zbog djelovanja čistog savijanja je:
gdje je: - naprezanje zbog savijanja, M - moment savijanja oko neutralne osi x, y - okomita udaljenost od neutralne osi x, Ix - moment tromosti ili moment inercije oko neutral osi x.
Maksimalno naprezanje na savijanje σmax pojavljuje se u točki koja je najudaljenija od neutralne osi ymax:
gdje je: - moment otpora presjeka.
Progib nosača proizlazi iz diferencijalne jednakosti elastične linije:
Uobičajene vrijednosti za maksimalne momente savijanja, progibe, momente tromosti i momente otpora presjeka mogu se naći u tablicama.
Zamašnjak[uredi | uredi kôd]
Zamašnjak je teški kotač koji, kada se zavrti, velikim momentom tromosti ili inercije ublažuje nemirni rad stroja (zbog udarnih opterećenja drobilica, alatnih ili valjaoničkih strojeva i drugo), nakupljenom kinetičkom energijom svladava mrtve točke strojeva (na primjer parnoga stroja), ili služi za stabilizaciju gibanja vozila, satelita, projektila i drugo (zvrk). Obično je to željezni ili čelični puni kotač, ili mu je veći dio mase raspoređen po vijencu. U prošlom je stoljeću bilo pokušaja da se zamašnjak upotrijebi i za pogon vozila, na primjer žirobusa; na postajama bi se zamašnjak zavrtio elektromotorom, a među postajama bi se postupno iskorištavala njegova kinetička energija za pokretanje žirobusa. Danas se intenzivno radi na razvoju sustava za akumuliranje energije kočenja automobila KERS (akronim od engl. Kynetic Energy Recovery System), a jedan dio sustava zasnovan je na zamašnjaku.[7]
Zvrk[uredi | uredi kôd]
Zvrk ili čigra, u fizici, je svako tijelo određene mase koje se vrti oko svoje osi te zbog momenta tromosti ili inercije tu vrtnju (rotaciju) održava. Svojstvo održavanja vrtnje ima široku primjenu, od dječjih igračaka do raznovrsnih tehnoloških uređaja.[8]
Izvori[uredi | uredi kôd]
- ↑ moment inercije (moment tromosti), [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
- ↑ Circle. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ a b c Circular Half. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ a b Quarter Circle. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ a b Rectangular area. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ a b Triangular area. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ zamašnjak, [2] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
- ↑ zvrk, [3] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.















































