Skup
U matematici, skup se može shvatiti kao bilo koja kolekcija različitih apstraktnih objekata smatranim cjelinom. Iako se ovo čini jednostavnom idejom, skupovi su jedan od najvažnijih fundamentalnih koncepata u modernoj matematici.[1]:21 Matematička disciplina koja proučava moguće skupove, teorija skupova, je sadržajno bogata i aktivna.[2][3][4][5]
Teorija skupova, stvorena tek krajem 19. stoljeća, je danas sveprisutni dio matematičkog obrazovanja, te se stoga u većini zemalja uvodi već u osnovnoj školi. Teorija skupova se može shvatiti kao osnova nad kojom može biti izgrađena gotovo cijela matematika, te kao ishodište iz kojeg gotovo cijela matematika može biti izvedena. Ovaj članak predstavlja kratak i osnovni uvod u ono što matematičari zovu "intuitivna" ili "naivna" teorija - za više detalja pogledati naivna teorija skupova. Za rigorozniji i moderniji aksiomatski pristup skupovima, razvijena je aksiomatska teorija skupova.

Na početku svog djela Beiträge zur Begründung der transfiniten Mengenlehre, Georg Cantor, principijelni tvorac teorije skupova, je napisao sljedeću definiciju skupa:[5] Pod terminom skup smatramo bilo koju kolekciju M određenih, različitih objekata m naše zamjedbe ili misli (koji će se zvati elementi skupa M) u cjelinu.
Objekte skupa također zovemo njegovim članovima ili elementima. Elementi skupa mogu biti raznih vrsta: brojevi, ljudi, slova abecede, drugi skupovi itd. Skupovi se dogovorno označavaju velikim slovima A, B, C, itd. Za dva skupa A i B kažemo da su jednaka i zapisujemo A = B ako imaju iste članove.
Skup, za razliku od multiskupa, ne može sadržavati više jednakih elemenata. Sve skupovne operacije čuvaju svojstvo jedinstvenosti elementa u skupu. Slično, redoslijed nabrajanja elemenata skupa je nebitan, za razliku od slijeda ili tupla.
Nemaju svi skupovi precizan opis - neki mogu jednostavno biti proizvoljne kolekcije, bez nekog jasno izraženog "pravila" koje kazuje koji su elementi unutar ili van skupa.
Neki skupovi mogu biti opisani riječima, na primjer:
- A je skup čiji su članovi prva četiri cijela broja.
- B je skup čiji su članovi boje hrvatske zastave.
Dogovorno se skup također može definirati eksplicitnim nabrajanjem svih elemenata između vitičastih zagrada, na primjer:
- C = {4, 2, 1, 3}
- D = {crvena, bijela, plava}
Dva različita opisa mogu definirati isti skup. Na primjer, gore definirani skupovi A i C su identični, pošto imaju jednake članove. Skraćeni zapis A = C se koristi za izražavanje takve jednakosti. Slično, za gore definirane skupove vrijedi B = D.
Identitet skupa ne ovisi o redoslijedu nabrajanja elemenata skupa, kao i o mogućim ponavljanjima elemenata prilikom nabrajanja. Na primjer, {6, 11} = {11, 6} = {11, 11, 6, 11}.
Za skupove s mnogo elemenata ponekad se koristi skraćena lista. Na primjer, prvih tisuću pozitivnih cijelih brojeva se mogu opisati simboličkom kraticom:
- {1, 2, 3, ..., 1000},
pri čemu specijalni simbol od tri točke (...) označava da se lista nastavlja na podrazumijevani način.
Slično se skup parnih brojeva može opisati notacijom:
- {2, 4, 6, 8, ... }.
Složeniji skupovi se ponekad opisuju različitom notacijom. Na primjer, skup F čiji su članovi prvih dvadeset brojeva koji su za četiri manji od kvadrata cijelog broja, može biti opisan na sljedeći način:
- F = { – 4 : n je cijeli broj; i 0 ≤ n ≤ 19}
U ovom opisu, dvotočka (:) znači "takav da", i matematičari interpretiraju ovaj opis kao "F je skup svih brojeva oblika – 4, takvih da je n cijeli broj u opsegu od 0 do 19 uključivo." (Ponekad se umjesto dvotočke koristi okomita crta |.)
Ako nešto jest ili nije element nekog pojedinačnog skupa, tada to simboliziramo sa odnosno . Na primjer, u odnosu na već definirane skupove, vrijedi:
- i (budući da je 285 = 17² − 4); ali
- i .
Svaki gore opisan skup ima konačan broj članova - na primjer, skup A ima četiri člana, dok skup B ima tri člana.
Skup također može imati nula članova. Takav skup zove se prazni skup i označava simbolom ø. Na primjer, skup A svih trostranih kvadrata ima nula članova, i stoga je A = ø. Poput broja nula, iako naizgled trivijalan, prazni se skup pokazao kao poprilično važan u matematici.
Skup također može imati beskonačan broj članova - na primjer, skup prirodnih brojeva je beskonačan.
Kaže se da su dva skupa ekvipotentna (imaju isti kardinalitet ili su jednakobrojni ili su bijektivni) ako postoji bijekcija iz jednoga skupa u drugi skup. Relacija ekvipotencije je relacija ekvivalencije, pa se skupovi svrstavaju u disjunktne klase - klasa kojoj pripada skup S zove se kardinalni broj skupa S i oznčava se sa ili card S ili #S.
Ako je svaki član skupa A također član skupa B, tada se za A kaže da je podskup od B, piše se , te izgovara A je sadržan u B. Može se, također, zapisati što se čita kao B je nadskup od A, B uključuje A ili B sadrži A. Relacija između skupova uspostavljenu sa zove se inkluzija.
Ako je A podskup i nije jednak skupu B, tada se za A kaže da je pravi podskup skupa B, zapisuje s (A je pravi podskup od B) ili (B je pravi nadskup od A). Međutim, u nekoj literaturi ovi se simboli čitaju isto kao i i , te se stoga češto preferira korištenje eksplicitnijih simbola i za prave podskupove i nadskupove.
Primjeri:
- Skup svih žena je pravi podskup skupa svih ljudi.
Prazni skup je podskup svakog skupa i svaki skup je sam svoj podskup:
Neki istaknuti skupovi imaju izuzetnu matematičku važnosti i toliko se često koriste da su dobili posebna imena i notaciju. Jedan od njih je već spomenuti prazni skup. Neki od ostalih su:
- označava skup svih prostih brojeva.
- označava skup svih prirodnih brojeva. Drugim riječima, = {1, 2, 3, ...}, ili rjeđe = {0, 1, 2, 3, ...}.
- označava skup svih cijelih brojeva (bilo pozitivnih, negativnih ili nule). Stoga je = {..., -2, -1, 0, 1, 2, ...}.
- označava skup svih racionalnih brojeva (tj. skup svih pravih i nepravih razlomaka). Stoga je = { : a,b i b ≠ 0}. Na primjer, i . Svi cijeli brojevi su u ovom skupu jer se svaki cijeli broj a može izraziti kao razlomak .
- je skup svih realnih brojeva. Ovaj skup uključuje sve racionalne i iracionalne brojeve (tj. brojeve koji se ne mogu zapisati u obliku razlomka, kao što su i √2).
- je skup svih kompleksnih brojeva.
Svaki od ovih skupova brojeva je beskonačan, premda vrijedi , iako se prosti brojevi općenito koriste manje od ostalih skupova izvan teorije brojeva i srodnih disciplina.
Međutim, ne postoji samo jedna vrsta beskonačnosti. Za skup koji je ekvipotentan (jednakobrojan) sa skupom prirodnih brojeva kažemo da je prebrojivo beskonačan (kraće prebrojiv), a "veći" skupovi su neprebrojivo beskonačni (kraće neprebrojivi).
Prebrojivo beskonačni skupovi su, na primjer, skupovi , kao i skup svih prirodnih brojeva koji su parni, neparni, djeljivi s 3, djeljivi 4, itd. Primjeri neprebrojivo beskonačnih skupova su i .
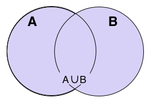
Postoji nekoliko načina za konstruiranje novih skupova od već postojećih. Dva se skupa mogu "zbrojiti". Unija skupova A i B, označena s A U B, je skup svih elemenata koji su članovi ili skupa A ili skupa B.
Primjeri:
- {1, 2} U {crvena, bijela} = {1, 2, crvena, bijela}
- {1, 2, zelena} U {crvena, bijela, zelena} = {1, 2, crvena, bijela, zelena}
- {1, 2} U {1, 2} = {1, 2}
Neka osnovna svojstva unije:
- A U B = B U A
- A je podskup skupa A U B
- A U A = A
- A U ø = A
Novi se skup također može konstruirati određivanjem "zajedničkih" elemenata obaju skupova. Presjek skupova A i B, označen s A ∩ B, je skup svih elemenata koji su članovi i skupa A i skupa B. Ako je A ∩ B = ø, tada za A i B kažemo da su disjunktni.
Primjer:
- {1, 2} ∩ {crvena, bijela} = ø
- {1, 2, zelena} ∩ {crvena, bijela, zelena} = {zelena}
- {1, 2} ∩ {1, 2} = {1, 2}
Neka osnovna svojstva presjeka:
- A ∩ B = B ∩ A
- A ∩ B je podskup skupa A
- A ∩ A = A
- A ∩ ø = ø
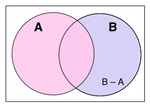
Dva se skupa također mogu "oduzeti". Relativni komplement skupa A u skupu B (još se koristi i naziv skupovna razlika skupova B i A), označeno s B − A, (ili B \ A), je skup svih elemenata koji su članovi skupa B, ali nisu članovi skupa A. Potrebno je uočiti da je valjana operacija "oduzimanja" članova koji nisu u skupu, poput micanja elementa zelena iz skupa {1,2,3} - takva operacija nema učinka.
U određenim postavkama, svi skupovi koji se promatraju, smatraju se podskupovima nekog danog univerzalnog skupa U. U takvim slučajevima, U − A zove se apsolutni komplement ili jednostavno komplement skupa A, i označava s A′, AC ili .
Primjeri:
- {1, 2} − {crvena, bijela} = {1, 2}
- {1, 2, zelena} − {crvena, bijela, zelena} = {1, 2}
- {1, 2} − {1, 2} = ø
- Ako je U skup svih cijelih brojeva, P skup parnih brojeva, a N skup svih neparnih brojeva, tada komplement skupa P u U iznosi N, ili ekvivalentno, P′ = N.
Neka osnovna svojstva komplementa:
- A U A′ = U
- A ∩ A′ = ø
- (A′ )′ = A
- A − A = ø
- A − B = A ∩ B′
- ↑ Elementarna matematika I (PDF). Prirodoslovno-matematički fakultet. Zagreb. 2018. Inačica izvorne stranice arhivirana 19. prosinca 2019. Pristupljeno 8. travnja 2021.CS1 održavanje: bot: nepoznat status originalnog URL-a (link)
- ↑ Teorija skupova (PDF). Sveučilište u Zagrebu. Siječanj 2015. Inačica izvorne stranice (PDF) arhivirana 24. srpnja 2019. Pristupljeno 24. listopada 2020.
- ↑ Halmos, Paul R. (Paul Richard), 1916-2006,. Naive set theory. New York. ISBN 0-387-90092-6CS1 održavanje: dodatna interpunkcija (link) CS1 održavanje: više imena: authors list (link)
- ↑ Stoll, Robert Roth. 1979, ©1963. Set theory and logic. Dover Publications. New York. ISBN 0-486-63829-4 Provjerite vrijednost datuma u parametru:
|date=(pomoć) - ↑ a b Allenby, R. B. J. T.,. 1991. Rings, fields, and groups : an introduction to abstract algebra 2nd ed izdanje. E. Arnold. London. ISBN 978-0-340-54440-2
|edition=sadrži dodatni tekst (pomoć)CS1 održavanje: dodatna interpunkcija (link) CS1 održavanje: više imena: authors list (link)