Savijanje





*raspodjela normalnog naprezanja po visini poprečnog presjeka linearna;
*sve točke presjeka jednako udaljene od neutralne osi presjeka imaju isto normalno naprezanje;
*u neutralnoj ravnini normalna naprezanja jednaki su nuli;
*najveća normalna naprezanja imaju vlakna najudaljenija od neutralne osi presjeka;
*neutralna os presjeka dijeli presjek na zonu vlaka i zonu tlaka.
Savijanje ili fleksija (engl. bending, flexure) je opterećenje koje djeluje okomito na uzdužnu os nosača. Za razliku od osnog opterećenja (vlak i tlak), pri savijanju štapa deformira se uzdužna os štapa. Deformirana uzdužna os zove se elastična linija ili progib. Razlikuje se čisto savijanje i poprečno savijanje. Pri čistom savijanju sve su komponente unutrašnjih sila jednake nuli, osim momenta savijanja. Pri poprečnom savijanju osim momenta savijanja pojavljuje se još i poprečna sila koja uzrokuje smicanje. Čisto savijanje zove se još i savijanje spregovima, a poprečno savijanje, savijanje silama. Moment savijanja uzrokuje normalna naprezanja σ koja se zamišljaju razdijeljenima po presjeku razmjerno udaljenosti od neutralne osi. Neutralna os prolazi kroz težište promatranog presjeka. Klasična jednakost koja određuje naprezanje u gredi zbog djelovanja čistog savijanja je:
gdje je: - naprezanje zbog savijanja, M - moment savijanja oko neutralne osi x, y - okomita udaljenost od neutralne osi x, Ix - moment tromosti ili moment inercije oko neutral osi x.
Maksimalno naprezanje na savijanje σmax pojavljuje se u točki koja je najudaljenija od neutralne osi ymax:
gdje je: - moment otpora presjeka.
Progib nosača proizlazi iz diferencijalne jednakosti elastične linije:
Uobičajene vrijednosti za maksimalne momente savijanja, progibe, momente tromosti i momente otpora presjeka mogu se naći u tablicama.
Povijest[uredi | uredi kôd]
Već na početku razvoja civilizacije, kad su se počele graditi veće zgrade, hramovi, mostovi, brodovi, jednostavni strojevi i naprave, bilo je potrebno da se sakupe podaci o svojstvima pojedinih konstrukcijskih materijala i oblika tijela. Bez sumnje su postojala iskustvena pravila o određivanju mjera pojedinih dijelova konstrukcija, jer bi bez njih bilo nemoguće izgraditi veličanstvene građevine i spomenike izgrađene još u starom vijeku. Osobito su se svojim graditeljstvom isticali graditelji Rimskog Carstva. Poznate su njihove palače, hramovi, arene, bazilike, akvedukti, te katapulti i drugi ratni i radni strojevi. Nešto o metodama njihova graditeljstva poznato je iz knjige De architectura libri decem od Marka Poliona Vitruvija. Najveći dio znanja koji su sakupili stari Grci i Rimljani i drugi narodi izgubljen je u toku ranoga srednjeg vijeka.
Prve značajne pokuse o ponašanju i čvrstoći materijala obavio je Leonardo da Vinci na prijelazu iz 15. u 16. stoljeće. On je ispitivao čvrstoću žice, greda i stupova. Došao je do ispravnog zaključka da je čvrstoća grede na dva oslonca razmjerna (proporcionalna) širini i obrnuto razmjerna rasponu. Nije zabilježeno da li je ispitivao utjecaj visine grede. Galileo Galilei je prvi pokušao da analitički odredi čvrstoću pojedinih dijelova konstrukcija. Utvrdio je da čvrstoća geometrijski sličnih tijela opada s porastom dimenzija. Poznata su njegova razmatranja o savijanju štapa. On je pogrešno pretpostavio da su sile (naprezanje) pri savijanju jednoliko raspodijeljene po visini presjeka grede i da se greda pri lomu okreće oko najniže točke oslonca. Uz tu pretpostavku ravnoteža momenata unutrašnjih i vanjskih sila oko ukliještenog kraja pravokutne (duljine l, širine b i visine h) konzole daje:
Točno rješenje glasi:
Galilejevo rješenje razlikuje se samo za konstantu od točnog rješenja. Galileo je objavio u djelu Discorsi e dimostrazioni matematische intorno a due nuove scienze attenenti alla meccanica & i movimenti locali (Leiden, 1638).
Problem savijanja grede obrađivao je i Edme Mariotte. On je u radu objavljenom 1690. zadržao pretpostavku da neutralna linija prolazi kroz donji brid presjeka, ali je uveo pretpostavku da naprezanja linearno rastu došao je do rješenja:
To je rješenje bliže točnomu od Galilejeva. Antoine Parent (16. rujna 1666. – 26. rujna 1716.) je također razmatrao savijanje grede. On je 1713. objavio dva rada. U prvome je pokazao da Mariotteovo rješenje može vrijediti samo za pravokutan presjek i izveo je izraz za kružni presjek. U drugom radu je pošao od pretpostavke da neutralna os prolazi kroz sredinu presjeka i došao do ispravnog rješenja. Njegov je rad, međutim, ostao nezapažen, pa su se mnogi inženjeri i dalje služili Mariotteovim rješenjem. Točno rješenje problema savijanja grede izveo je 1773. Charles-Augustin de Coulomb ne poznavajući Parentovo rješenje. On je 1784. riješio problem uvijanja okruglog štapa i uveo pojam modula smicanja.
Zakon linearne ovisnosti opterećenja i pomaka, odnosno naprezanja i deformacije postavio je 1660. Robert Hooke na temelju pokusa s oprugama. Međutim, taj zakon, poznat kao Hookeov zakon, objavljen je tek 1678. u knjizi De potentia restitutiva, s objašnjenjem kakva sila, takvo produljenje. Thomas Young je 1807. matematički izveo Hookeov zakon za jednoosno rastezanje i uveo pojam modula elastičnosti, koji se po njemu naziva i Youngov modul elastičnosti. Taj je zakon 1828. dopunio Siméon Denis Poisson i uveo pojam koeficijenta poprečne konstrukcije pri rastezanju, koji se po njemu naziva Poissonov koeficijent ili Poissonov omjer.
Znatno su pridonijeli razvoju teorije elastičnosti i analitičkim metodama o nauci o čvrstoći švicarski matematičari, braća Jakob i Johann Bernoulli. Oni su razmatrali deformacije grede pri savijanju. Jacob Bernoulli je uveo pretpostavku da pri savijanju poprečni presjeci ostaju ravni. On je 1694. utvrdio da je zakrivljenost elastične linije sukladna (proporcionalna) momentu savijanja. Daniel Bernoulli, Johannov sin, prvi je izveo diferencijalnu jednakost poprečnih vibracija štapa. Leonhard Euler, učenik Daniela Bernoullija, također je proučavao elastične linije. On je 1744. izveo izraz za kritičnu silu izvijanja vitkog štapa. Augustin Louis Cauchy je 1822., u radu koji je predložio Francuskoj akademiji znanosti, po prvi put odredio prostorno stanje naprezanja i izveo jednakosti ravnoteže diferencijalnog elementa. Prvi rad iz teorije ploča objavio je Claude-Louis Navier 1820. On je također prvi dao opći pristup rješavanju statički neodređenih zadataka. Teoriju savijanja ploča razrađivali su dalje Siméon Denis Poisson, Gustav Robert Kirchhoff i drugi. D. J. Žuravski je izveo 1844. izraz za posmična naprezanja pri savijanju grede. Emil Winkler je 1858. riješio problem savijanja debeloga zakrivljenog štapa metodama nauke o čvrstoći. Točno rješenje tog problema dao je 1881. M. Golovin. Uvijanja nekih neokruglih presjeka riješio je 1852. Adhémar Barré de Saint-Venant. Godine 1857. Émile Clapeyron izveo je jednakost triju momenata (Clapeyronova jednakost). James Clerk Maxwell je 1870. izveo poučak o recipročnosti uplivnih koeficijenata (Maxwellov poučak), a Carlo Alberto Castigliano je 1873. izveo svoj prvi poučak. Christian Otto Mohr je objavio rad o kružnicama naprezanja 1895.[1]
Moment tromosti[uredi | uredi kôd]
Moment tromosti ili moment inercije (znak I ili J) je fizikalna veličina koja opisuje tromost ili inerciju čestice ili krutoga tijela pri promjeni brzine ili smjera vrtnje; jednaka je zbroju umnožaka mase m i kvadrata udaljenosti r od osi rotacije svake čestice koja čini tijelo:
Moment tromosti nekog tijela ovisi o obliku tijela, raspodjeli mase, položaju osi rotacije. Primjerice, ako je m masa tijela, r njegov polumjer, a os rotacije ujedno i os simetrije, moment inercije na primjer šupljega valjka ili prstena iznosi:
homogeno ispunjenoga valjka ili kružne ploče:
homogeno ispunjene kugle:
Moment tromosti homogeno ispunjenoga štapa kojemu je os rotacije okomita na dužinu štapa nalazi se na polovici dužine štapa:
a na kraju je štapa:
gdje je: r - duljina štapa. Mjerna je jedinica momenta tromosti kilogram puta kvadratni metar (kg m2).[2]
Momenti tromosti nekih presjeka[uredi | uredi kôd]
| Opis | Slika | Moment tromosti | Primjedba | Literatura |
|---|---|---|---|---|
| puni kružni presjek (šipka) s polumjerom r |  |
[3] | ||
| prsten (cijev) s unutarnjim polumjerom r1 i vanjskim polumjerom r2 | 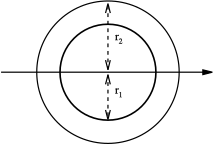 |
Za tanke cijevi, i .
Možemo reći da , i zbog ta zagrada se može pojednostaviti u . Konačno, za tankostijenu cijev proizlazi, . |
||
| puni kružni isječak s kutom θ u radijanima i polumjerom r, s obzirom na os kola prolazi kroz težište i središte kružnice |  |
Jednakost vrijedi samo za 0 ≤ ≤ | ||
| puni polukrug s polumjerom r u odnosu na vodoravni pravac koji prolazi kroz težište |  |
[4] | ||
| puni polukrug s polumjerom r u odnosu na vodoravni pravac koji prolazi kroz osnovu |  |
Udaljenost između težišta i osnove je | [4] | |
| puni polukrug s polumjerom r u odnosu na okomiti pravac koji prolazi kroz težište |  |
[4] | ||
| puna četvrtina kruga s polumjerom r s obzirom na središte kruga. |  |
[5] | ||
| puna četvrtina kruga s polumjerom r s obzirom na pravac prolazi kroz težište |  |
Udaljenost između težišta i baze je | [5] | |
| puna elipsa s poluosima a (uzduž osi x) i b |  | |||
| puni pravokutnik s osnovicom a i visinom h u odnosu na pravac koji prolazi kroz težište |  |
[6] | ||
| puni pravokutnik s osnovicom a i visinom h u odnosu na pravac koji prolazi kroz osnovicu |  |
[6] | ||
| puni trokut s osnovicom b i visinom h u odnosu na pravac koji prolazi kroz težište |  |
[7] | ||
| puni trokut s osnovicom b i visinom h u odnosu na pravac koji prolazi kroz osnovicu |  |
[7] | ||
| puni šesterokut sa stranicom a, pravac prolazi kroz težište ili središte |  |
Isto vrijedi i za okomiti pravac. |
Elastična linija i progib[uredi | uredi kôd]

Elastična linija nosača ili progibna linija nosača je uzdužna os štapa (težišna linija nosača) u deformiranom (savijenom) obliku. Najveća deformacija nosača ne smije biti veća od unaprijed zadane vrijednosti (uvjet krutosti). Poprečni presjeci pomiču se i istodobno zaokreću oko neutralne osi i pri tome ostaju okomiti na savijenu os štapa. Elastična linija ili progibna linija nosača je savijena (deformirana) uzdužna os nosača. Progib nosača je pomak težišta presjeka u smjeru okomitom na nedeformiranu os nosača (štapa). Kut zaokreta je kut za koji se neki presjek zaokrene u odnosu na svoj prvobitni položaj.[8]

Jednostavna greda sa silom u sredini[uredi | uredi kôd]
Elastični progib δC (u mm) u sredini jednostavne grede (točka C), koja je opterećena silom F u središtu, a nalazi se na 2 jednostavna oslonca, dat je izrazom:
gdje je:
- = sila koja djeluje u sredini grede (N);
- = duljina između oslonaca (mm);
- = Youngov modul elastičnosti (N/mm2);
- = moment tromosti ili moment inercije (mm4).
Progib u bilo kojoj točki x, uzduž grede, koja je udaljena od jednog oslonca, može se izračunati koristeći jednakost:
za
Izvori[uredi | uredi kôd]
- ↑ "Tehnička enciklopedija" (Nauka o čvrstoći), glavni urednik Hrvoje Požar, Grafički zavod Hrvatske, 1987.
- ↑ moment inercije (moment tromosti), [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
- ↑ Circle. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ a b c Circular Half. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ a b Quarter Circle. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ a b Rectangular area. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ a b Triangular area. eFunda. Pristupljeno 30. prosinca 2006.
- ↑ "Strojarski priručnik", Bojan Kraut, Tehnička knjiga, Zagreb 2009.


















































