Prvi Keplerov zakon
Prvi Keplerov zakon glasi:
| Planeti se oko Sunca kreću po eliptičnim putanjama; u zajedničkom žarištu tih elipsa nalazi se Sunce. |

Na prikazanoj slici elipsa predstavlja putanju nekog planeta. Linearni ekscentricitet je:
a numerički ekscentricitet je:
Iz toga proizlazi:
gdje se naziva parametrom elipse.
Po definiciji elipse, . Iz trokuta , primjenom kosinusnog poučka i supstitucijom parametra elipse, slijedi da je:
i to bi bila jednadžba planetske putanje (jednadžba elipse), odnosno matematski izraz prvoga Keplerova zakona. Iz te se jednadžbe vidi ovisnost udaljenosti planeta od Sunca o kutu koji se naziva pravom anomalijom planeta.
Kad je , tada je , pa iz toga proizlazi definicija parametra planetske putanje kao radijus-vektora planeta koji je okomit na glavnu os elipse.
Karakteristične točke planetske putanje su afel i perihel (označene na slici s i ). Afel je točka u kojoj je planet najudaljeniji od Sunca, a perihel je točka u kojoj je planet najbliži Suncu. Ako je srednja udaljenost planeta od Sunca, onda proizlazi da su:
Geometrija elipse kod prvog Keplerovog zakona[uredi | uredi kôd]

Kada je θ = 0°, ili perihel (točka u kojoj je planet najbliži Suncu) vrijedi:
Kada je θ = 90° ili θ = 270°, udaljenost između Sunca i planeta je jednaka maloj poluosi elipse b.
Kada je θ = 180°, ili afel (točka u kojoj je planet najudaljeniji od Sunca) vrijedi:
Između velike poluosi a, perihela rmin i afela rmax vrijedi:
Između male poluosi b, perihela rmin i afela rmax vrijedi:
Između parametra elipse p, perihela rmin i afela rmax vrijedi:
Između numeričkog ekscentriciteta ε, perihela rmin i afela rmax vrijedi:
Površina elipse je:
Poseban slučaj elipse je kružnica kada je ε = 0, što daje r = p = rmin = rmax = a = b i A = π r2.
Svojstva elipse[uredi | uredi kôd]

Kružnica ima jednu važnu točku, središte. Elipsa ima takve dvije točke, koje se zovu žarišta. Na slici su žarišta označena slovima F1 i F2. Označimo li na krivulji koju god točku, recimo X, i spojimo je sa žarištima. Ako zbrojimo ove dvije dužine, označene slovima r1 i r2 dobit ćete dužinu AB, koja se zove velika os elipse. Točke A i B zovu se tjemena. U polovištu velike osi je središte. Polovina velike osi zove se poluos elipse i bilježi se obično slovom a. Udaljenost središta od žarišta, podijelimo s polovinom velike osi AS i dobivamo broj koji se zove ekscentricitet elipse e. Ako je elipsa vrlo slična kružnici, kao što je to slučaj kod staze planeta, onda su žarišta F1 i F2 blizu jedno drugome i ekscentricitet je vrlo malen. Zamislimo sada da se Sunce nalazi u žarištu F1, a planet se giba po elipsi. Njegova udaljenost od Sunca neprestano mijenja. Kad je u tjemenu A, onda je najbliži Suncu, zato se ta točka u stazi planeta zove perihel (grč. peri: blizina, helios: Sunce). Dok putuje od perihela do točke B sve se više udaljuje od Sunca. Najveća je udaljenost F1B. Kad planet stigne u točku B, onda je najdalje od Sunca, zato se točka B zove afel (riječ složena od apo: od i helios: Sunce). Planet se nije zaustavio u afelu nego nastavlja svoje gibanje po elipsi prema perihelu. Time se opet približava Suncu.[1]
U vrijeme Johannesa Keplera nije bilo još poznato koliko je Zemlja udaljena od Sunca, pa se nisu znale ni ostale udaljenosti u svemiru. Ipak se moglo prema starijim teorijama, a onda i prema novijim opažanjima, dosta točno ustanoviti koliko puta je neki planet bliže ili dalje od Sunca, nego li Zemlja. Čim je planet bliži Suncu, tim je kraće vrijeme njegova obilaska. Osim toga, retrogradno gibanje pokazuje kako velikom se vidi staza Zemlje gledana s tog planeta. Na toj osnovi su astronomi već u staro doba dosta dobro mogli odrediti i udaljenosti planeta od Sunca uzevši udaljenost Zemlje kao jedinicu. Tablica ispod pokazuje Kopernikove i današnje rezultate (osnova je udaljenost Zemlje od Sunca aZ ili astronomska jedinica):[2]
| Odnos a/aZ | Kopernik | Danas |
|---|---|---|
| Merkur | 0.376 | 0.387 |
| Venera | 0.7196 | 0.723 |
| Mars | 1.52 | 1.524 |
| Jupiter | 5.217 | 5.203 |
| Saturn | 9.184 | 9.54 |
Prvi Keplerov zakon i planetarne putanje[uredi | uredi kôd]


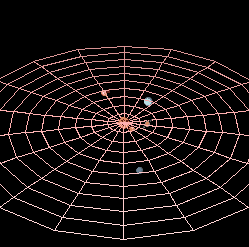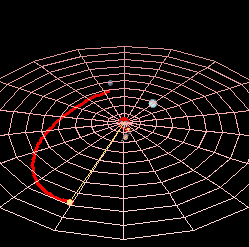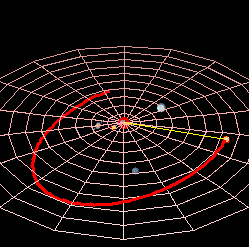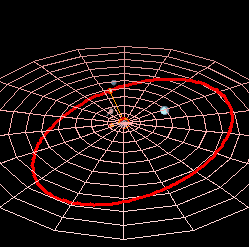

Prvi Keplerov zakon ustanovljuje geometrijske osobine planetarnih putanja. Kepler je našao da su staze elipse, a da se Sunce nalazi u jednom od žarišta. Kako je Sunce zajedničko svim planetima, tako je Sunce u žarištu koje je zajedničko svim eliptičnim stazama. To je jedini uvjet i nema daljih ograničenja, pa položaj putanje u prostoru može biti veoma raznolik. Na skicama koje prikazuju dvije ili više planetarnih putanja, one se nalaze u istoj ravnini. Općenito, velike poluosi dviju elipsi ne podudaraju se ni po smjeru, ni po veličini, ni po ravninama u kojima se nalaze.
Veličina i izduženost elipse određena je velikom poluosi a i ekscentricitetom e. Velika poluos a ujedno je i srednja udaljenost točke na elipsi od jednog žarišta (planeta od Sunca). Kada je tijelo najdalje od Sunca u afelu, njegova je provodnica (radijus - vektor) najveća:
Kada je planet Suncu najbliže (kada je u perihelu), tada mu je provodnica najmanja:
Aritmetička sredina tih udaljenosti ili srednja udaljenost jednaka je velikoj poluosi a:
Izduženost putanje iskazuje se numeričkim ekscentricitetom ε koji je jednak:
ε je bezdimenzionalna veličina. Sa smanjenjenjem ekscentriciteta (ε → 0) elipsa prelazi u kružnicu, a njezina velika poluos prelazi u polumjer kružnice. Ulogu srednje udaljenosti ima tada, naravno, sam polumjer kružnice. S druge strane, s povećanjem ekscentriciteta (ε → 1) elipsa prelazi u parabolu. Za hiperbolu vrijedi ε > 1. Parabola i hiperbola nisu zatvorene krivulje.
Veličine planetarnih putanja[uredi | uredi kôd]
Položaj planetarne putanje u prostoru treba odrediti pomoću poznatih orijentira. Zato se upotrebljava ravnina ekliptike i proljetna točka. Kut između ravnine u kojoj se nalazi staza tijela i ravnine ekliptike zove se nagib ili inklinacija (oznaka: i). Dvije se ravnine sijeku u pravcu na kojemu su dvije točke istaknute - one u kojima planetarna putanja probada ravninu ekliptike: uzlazni čvor Ω (u njemu tijelo u svom godišnjem gibanju prelazi s južne strane ekliptike na sjevernu) i silazni čvor Ʊ (u njemu tijelo u svom godišnjem gibanju prelazi sa sjeverne strane ekliptike na južnu). Položaj uzlaznog čvora zadaje se ekliptičkom dužinom uzlaznog čvora Ω. S mjerama i i Ω orijentirana je ravnina gibanja nebeskog tijela u prostoru. Da bi se pak u toj ravnini orijentirala elipsa, bilježi se položaj njezina perihela. U tu svrhu služi argument perihela π, kut od uzlaznog čvora do velike poluosi koja sadrži perihel. Longitudom perihela naziva se ukupan kut ω = Ω + π.
Da bi se pratilo gibanje nebeskog tijela, potrebno je dodati podatak o zvjezdanom (sideričkom) ophodnom vremenu P i o trenutku to u kojemu tijelo prolazi perihelom. Dakle, za opis geometrijskih svojstava planetarnih putanja - veličine elipse, oblika elipse, njezine orijentacije i načina gibanja tijela - potrebno je 7 veličina: a, e, i, Ω, ω, P i to. To su veličine planetarnih putanja.
Analiza planetarnih putanja[uredi | uredi kôd]
Većina planeta ima slabo izdužene planetarne putanje (staze), koje je na malom crtežu okom teško razlikovati od kružnice. Tako Zemljina putanja s ε = 0.001673 ima veliku poluos a = 149.597 ∙ 106 km, malu poluos b = 149.577 ∙ 106 km, najmanju udaljenost od Sunca rmin = 147.1 ∙ 106 km i najveću udaljenost od Sunca rmax = 152.1 ∙ 106 km.
Staze planetoida u prosjeku su jače izdužene os planetnih putanja. U kometa je šarolikost mnogo veća. Neki kometi imaju numerički ekscentricitet ε blizak jedinici.
Razlike se opažaju i u nagibima planetarnih putanja. Plutonova i Merkurova staza najviše se od svih planeta otklanjaju od Zemljine putanje. Kod Plutona to dovodi do zanimljive posljedice. Naime, crtaju li se staze Neptuna i Plutona projicirane u istu ravninu, čini se da se zbog izduženosti Plutonove staze te dvije putanje sijeku, te da se dva planeta mogu i sudariti. Neptun je zaista u nekim razdobljima dalje od Sunca nego Pluton (na primjer kao od 1980. do 1999.). No kako se ravnine putanja Neptuna i Plutona sijeku pod kutom od kojih 15°, to su staze uvijek daleko jedna od druge. Stoga se oni nikada ne mogu sudariti.
Putanje planetoida nagnute su prema ekliptici za više desetaka stupnjeva, ravnine kometa mogu pak sjeći ekliptiku pod bilo kojim kutom. Kada je kut inklinacije veći od 180°, kaže se da je putanja nebeskog tijela i njegova revolucija retrogradna; projicirajući takvu stazu na ravninu ekliptike, vidjelo bi se da se tijelo giba oko Sunca u suprotnom smislu od Zemlje i ostalih planeta. Svi planeti i planetoidi imaju direktnu revoluciju. Fizički različite vrste tijela u Sunčevu sustavu se grupiraju po geometrijskim svojstvima putanja. Do razlika u vladanju nebeskih tijela došlo je u toku razvoja Sunčeva sustava.
Općenito, veličine planetarnih putanja pojedinog člana Sunčeva sustava neprestano se mijenjaju. Promjena tih veličina kod Zemlje mogla je u prošlosti, u dugim geološkim razdobljima, utjecati na klimatske promjene.
Zapazimo još da se velika poluos (linija koja povezuje najbliži i najudaljeniji položaj tijela od Sunca, perihel i afel), nazvana još i linija apsida, ne podudara s linijom koja povezuje zimsku i ljetnu točku. Razlika se u stvari stalno povećava, jer se linija apsida zakreće u liniji putanje; zakreće se u smjeru gibanja Zemlje, pa Zemlji treba više vremena da ponovo stigne u perihel, nego što joj treba da ponovi svoj položaj prema zvijezdama. Drugim riječima, zvjezdana (siderička) godina kraća je od vremena prolaska Zemlje perihelom. To razdoblje traje 365 d 6 h 13 min 53 s = 365.25964 d i zove se anomalistička godina (godina).






























