Rezonancija









Rezonancija (kasnolat. resonantia: odjek, odzvuk) je titranje fizikalnoga sustava pobuđenog nekom vanjskom periodičnom silom kojoj se frekvencija podudara sa svojstvenom (vlastitom, karakterističnom) frekvencijom sustava.[1] Rezonancija nastaje kod sustava koji prisilno titra kada se pri određenoj frekvenciji pobude postiže maksimalna amplituda titranja. Izraženost rezonancije ovisi o prigušenju, to jest omjeru energije gubitaka i ukupne energije u sustavu.
Pojave rezonancije se uočavaju u mnogim područjima fizike: mehanici, akustici, elektrotehnici, atomskoj i nuklearnoj fizici. Na primjer u mehanici je se rezonanciji uočava kod vibriranja tijela oko njegove vlastite frekvencije vibracija. Mala i ponavljana pokretna sila proizvodi vibracije većih amplituda. Gibanje njihala primjer je pravilnog izmjenjivanja gibanja nazvanog oscilacija. Bilo da se njihalo njiše brzo ili sporo, prema i od, svaki potpuni njihaj treba isto vrijeme. Frekvencija njihanja ovisi samo o duljini užeta ili žice koja nosi masu koja se njiše na njihalu.
Pojam rezonancije povezan je s porastom jakosti (intenziteta) titraja kada se učestalost vanjske sile koja uzrokuje titraje podudara s učestalošću rezonantne frekvencije sustava. Tijekom tog procesa dolazi najčešće do naizmjenične pretvorbe jednog oblika energije u drugi, kao na primjer kinetičke u potencijalnu ili energije električnog polja u energiju magnetskog polja. Pojave vezane za rezonanciju mogu se, međutim, uočiti i u drugim fizikalnim sustavima. Prepoznatljivo je svojstvo rezonantnih sustava da, jednom pobuđeni, mogu samostalno titrati još neko vrijeme koje ovisi o prigušenju titrajnog sustava. U zamišljenom idealnom rezonantnom sustavu gdje nema prigušenja, rezonantni sustav bi nastavio titrati zauvijek.
Mehanička rezonancija[uredi | uredi kôd]
Za razliku od električnih rezonantnih sustava koji se temelje na električnim veličinama, mehanički rezonantni sustavi temelje se na mehaničkim veličinama kao što su, na primjer, sila i masa. Premda se mogu razmatrati fizikalno različiti mehanički rezonantni sustavi, najpoznatiji predstavnici ovakvih sustava su sustav utega i opruge te sustav njihala. Fizikalni sustav na koji ne djeluju vanjske periodične sile titra frekvencijama svojstvenima sustavu. Ako na sustav djeluju vanjske periodične sile frekvencijama različitim od svojstvenih, on će titrati u frekvencijama vanjskih sila, ali amplituda tih titraja bit će uvijek malena. Kada je frekvencija uzbudne sile upravo jednaka svojstvenoj frekvenciji sustava, amplituda je titranja velika, te nastaje rezonancija. Svojstvene frekvencije nekoga mehaničkog sustava ovise o njegovoj masi, dimenzijama i silama naprezanja koje u njem postoje. Za elastičnu šipku duljine l, mase m, podvrgnutu sili naprezanja f, karakteristične frekvencije νn dane su izrazom:
gdje je n - cijeli broj.
Mehanička rezonancija može izazvati neželjene posljedice u radu strojeva te njihovo oštećivanje, pa se pri projektiranju nastoji izbjeći. Također je važno i temeljenje strojeva da se oscilacije ne bi prenosile na građevinske elemente koji bi se u slučaju rezonancije također mogli oštetiti. Iz mehanike je pojam rezonancije prenesen i u druga područja fizike, gdje označuje niz analognih pojava kao što su električna, nuklearna, kvantnomehanička rezonancija i tako dalje.
Rezonantni sustav utega i opruge[uredi | uredi kôd]
Ovjesimo li uteg o prikladno učvršćenu oprugu, pomaknemo li zatim uteg iz ravnotežnog položaja i otpustimo ga, uteg će otpočeti periodičko gibanje tijekom kojeg će se naizmjence kinetička energija gibanja utega pretvarati u unutrašnju potencijalnu energiju opruge i obratno. Razmatanjem sila u rezonantnom sustavu utega i opruge dolazimo do sljedeće jednadžbe:
gdje je: m - masa utega, k - konstanta opruge, a x - pomak utega. Rješenje ove diferencijalne jednadžbe u stacionarnom stanju je periodička funkcija oblika:
koja se pojavljuje nakon probude, gdje je A - amplituda titranja, a
kružna frekvencija. Titrajni krug će, dakle, neprigušeno periodički zatitrati kružnom frekvencijom koja je određena veličinom mase utega i konstantom opruge. U stvarnosti valja uračunati određena prigušenja koja se javljaju u obliku trenja zraka (otpor sredstva) i energetskih gubitaka zbog promjene oblika opruge, te će stvarna rezonantna frekvencija biti nešto niža, a titranje će biti eksponencijalno prigušeno i ovisno o rezultantnom otporu trenja koji prouzrokuje energetske gubitke.
Ovakav rezonantni sustav u frekvencijskom području rezonancije ima i neke dodatne osobine. Pod utjecajem vanjske mehaničke sile dolazi do odziva sustava u obliku gibanja, gdje je brzina gibanja utega mjera tog odziva. U stvarnosti je takva brzina ograničena rezultantnim energetskim gubicima u mehaničkom titrajnom sustavu. Međutim, uz dovoljno male gubitke u titrajnom krugu brzina gibanja može i uz malu veličinu sile poprimiti velike vrijednosti (slabo prigušen titrajni sustav) što se vidi iz jednakosti:
gdje su: v i F - brzina gibanja, odnosno mehanička sila kao funkcije kružne frekvencije, Rm - rezultantno mehaničko trenje i ostalih gubici, m - masa utaga i k - konstanta opruge.
Rezonantni sustav njihala[uredi | uredi kôd]
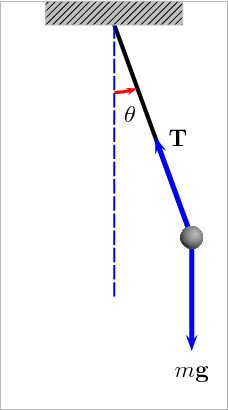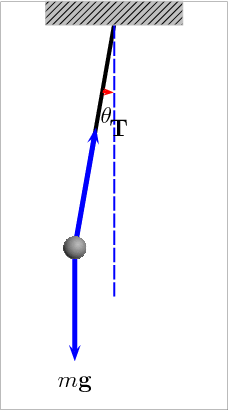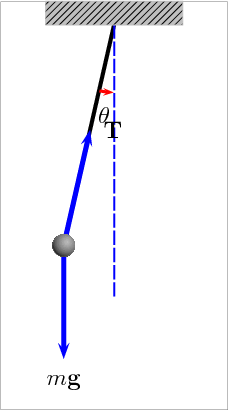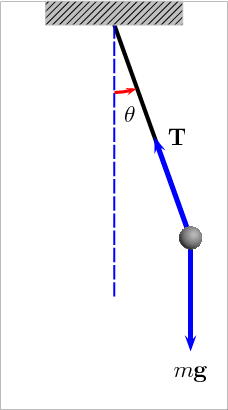
Ovjesimo li neku masu o nerastezljivu nit, pomaknemo li zatim masu iz ravnotežnog položaja i otpustimo je, ona će otpočeti periodičko gibanje tijekom kojeg će se naizmjence kinetička energija gibanja utega pretvarati u potencijalnu gravitacijsku energiju utega i obratno. Razmatanjem sila u rezonantnom sustavu njihala, a za male pomake mase u odnosu na duljinu niti, dolazimo do sljedeće jednadžbe:
gdje je m - ovješena masa, g - ubrzanje zemljine sile teže, l - duljina niti, a x - pomak mase iz ravnotežnog položaja. Rješenje ove diferencijalne jednadžbe u stacionarnom stanju je periodička funkcija oblika
koja se pojavljuje nakon probude, gdje je A - amplituda titranja, a
kružna frekvencija. Njihalo će, dakle, neprigušeno periodički zatitrati kružnom frekvencijom koja je ovisna o gravitacijskom ubrzanju i duljini niti. U stvarnosti valja uračunati utjecaj trenja zraka, te će stvarna rezonantna frekvencija biti nešto niža, a titranje će biti eksponencijalno prigušeno i ovisno o trenju do kojeg dolazi prilikom gibanja mase i niti kroz zrak.
Ostali mehanički rezonantni sustavi[uredi | uredi kôd]
Brojni su primjeri mehaničkih sustava koji ispoljavaju rezonantna svojstva, kao što su na primjer glazbene viljuške, različite šipke, odgovarajuće učvršćena užad i drugi. Razmatranje rezonantnih svojstava kod takvih fizikalnih sustava je, međutim, znatno složenije jer ovisi ne samo o veličini, masi i elastičnosti, već i o raspodjeli mase, te vrlo često i o pojavi stojnih valova kao oblika titranja. Rezonantne tvorevine mogu biti i veće cjeline kao dijelovi strojeva, uređaja ili građevinskih konstrukcija. Ekstremni primjer u tom smislu je razorno djelovanje rezonancije na mostu Tacoma Narrows Bridge u Washingtonu, SAD 1940. Vjetar odgovarajućeg smjera i brzine pobudio je most na gibanje (njihanje) te kako je frekvencija gibanja bila u blizini rezonantne frekvencije mosta, amplituda gibanja postajala je iz sata u sat sve veća, te konstrukcija mosta naposljetku nije izdržala i most se srušio.
Akustička rezonancija[uredi | uredi kôd]
Akustička rezonancija nastaje kada se na titranje pobudi zračni stupac u određenom prostoru i u njem stvore stojni valovi. Poželjna je kod glazbala sa žicama (rezonantne kutije, na primjer violine i gitare) te u određenim uvjetima u koncertnim dvoranama ili kazalištima, a nepoželjna u radnim prostorima kao što su tvorničke dvorane u kojima povećava buku. Akustički rezonatni sustavi su tvorevine unutar kojih titra zrak. To titranje se, u osnovi, može pojaviti u dva oblika. Prvi oblik se pojavljuje, na primjer, u zvučničkoj bas-refleksnoj kutiji gdje masa zraka u otvoru bas-refleksa stupa u rezonanciju s elastičnošću zraka zatvorenog u samoj zvučničkoj kutiji. Drugi oblik takvog titranja javlja se u obliku stojnog vala stupca zraka zatvorenog u dugoljast prostor s otvorom na vrhu i osnova je konstrukcije brojnih glazbenih instrumenata.
Električna rezonancija[uredi | uredi kôd]
Premda postoje brojne vrste fizikalno različitih vrsta titranja, posebno je zanimljiva pojava rezonancije u električnim titrajnim krugovima koja ima mnogobrojne primjene u elektrotehnici. Najjednostavniji titrajni električni sustav sastoji se od električne zavojnice i električnog kondezatora s odgovarajućim nazivnim električnim induktivitetom, odnosno električnim kapacitetom. Pobuđeni impulsom iz odgovarajućeg električnog izvora, titrajni krug će zatitrati na način da će energija određenom učestalošću naizmjence prelaziti sa zavojnice na kondenzator i natrag na zavojnicu. Tijekom tog procesa dolazi do naizmjenične pretvorbe energije magnetskog polja u zavojnici u energiju električnog polja u kondenzatoru i natrag u energiju magnetskog polja u zavojnici. Energija prelazi u obliku izmjenične električne struje periodičkog sinusoidalnog oblika i to one frekvencije koja je određena rezonantnim svojstvima titrajnog kruga.
Električni rezonantni sustav može biti predočen, na primjer, serijskim titrajnim krugom sastavljenim od idealnog induktiviteta L i idealnog kapaciteta C, gdje titrajni krug ne sadrži radne otpore koji bi uzrokovali gubitke energije. Pobudimo li takav titrajni krug na titranje, strujnim krugom će poteći struja kao odziv titrajnog kruga na pobudu. Prilike su za takav, neprigušen, slučaj općenito zadane integralno-diferencijalnom jednadžbom:
Rješenje ove diferencijalne jednadžbe u stacionarnom stanju je periodička funkcija oblika
koja se pojavljuje nakon probude, gdje je A amplituda titranja, a
kružna frekvencija. Titrajni krug će, dakle, neprigušeno periodički zatitrati kružnom frekvencijom koja je određena veličinom induktiviteta i kapaciteta. Ako je u titrajnom krugu prisutan i otpor, titrajni krug će zatitrati na nešto nižoj frekvenciji uz eksponencijalno prigušenje ovisno o rezultantnom otporu koji prouzrokuje energetske gubitke.
Električni rezonantni sustavi imaju svojstvo da im u frekvencijskom području rezonancije električna impedancija poprima ekstremne vrijednosti što ima i odgovarajući utjecaj na veličinu električne struje u strujnom krugu kao odziva na vanjsku pobudu. Električna impedancija serijskog titrajnog kruga bi u idealnim uvjetima na rezonantnoj frekvenciji postala jednaka nuli, a električna impedancija paralelnog titrajnog kruga u istim uvjetima beskonačno velika. Međutim, u stvarnim uvjetima postizanje ekstrema je ograničeno rezultantnim otporom gubitaka u titrajnom krugu (radni otpor zavojnice, odn. otpor izolacije kondenzatora) te je za slučaj serijskog titrajnog kruga električna struja u serijskom titrajnom krugu određena kao
gdje su: I, U i Z - električna struja, napon i impedancija kao funkcije kružne frekvencije, Rs - nadomjestni otpor gubitaka u serijskom spoju, L - induktivitet zavojnice i C - kapacitet kondenzatora u titrajnom krugu. Na samoj rezonantnoj frekvenciji električna struja u strujnom krugu bit će ograničena nadomjestnim otporom gubitaka Rs u serijskom spoju.
Kvantnomehanička rezonancija[uredi | uredi kôd]
Kvantnomehanički sustavi, na primjer molekule ili skupine molekula, također imaju vlastite vibracijske frekvencije, a rezonancija se pojavljuje kada energija pobuđivanja odgovara razlici energija dvaju mogućih energetskih stanja sustava. Amplituda, koja u tom slučaju odgovara vjerojatnosti prijelaza, naglo se povećava kada se energija pobuđivanja:
(gdje je: h - Planckova konstanta, a ν - frekvencija) približava razlici energija dvaju kvantnih stanja. Danas su u fizici poznate mnoge pojave koje se tumače kvantnomehaničkom rezonancijom, na primjer rezonantno zračenje, rezonantno raspršenje, nuklearna rezonancija, te je na tom načelu razrađeno više metoda za određivanje energetskih stanja sustava (elektronska paramagnetska rezonancija; nuklearna magnetska rezonancija).
Nuklearna magnetska rezonancija[uredi | uredi kôd]
Nuklearna magnetska rezonancija ili NMR je apsorpcija radiofrekvencijskoga zračenja pri prijelazu između kvantnih stanja atomskih jezgri neke tvari koja se nalazi u jakom magnetskom polju. Atomske jezgre mnogih elemenata imaju kutni moment nazvan spin (engl. spin: vrtnja), koji se pojednostavnjeno može shvatiti kao vrtnja jezgre oko vlastite osi. Tomu je spinu pridružen magnetski moment jezgre. U homogenom magnetskom polju os vrtnje jezgre otklonit će se pod nekim kutom s obzirom na smjer polja, pa će se jezgra ujedno okretati (precesirati) oko osi magnetskoga polja. U skladu sa zakonima kvantne mehanike, dopuštene su samo neke orijentacije u magnetskom polju. U najjednostavnijem slučaju, za atomske jezgre sa spinom ½ (atomske jezgre vodika, ugljika, fluora, fosfora), jedine su dvije moguće orijentacije spinskih kvantnih stanja paralelna i antiparalelna orijentacija s obzirom na smjer magnetskoga polja. Ako se zatim na precesirajuću jezgru primijeni rastuće radiofrekvencijsko zračenje, jezgra će apsorbirati zračenje onda kada frekvencija zračenja postane jednaka frekvenciji precesije jezgre, te će jezgra pritom prijeći u višu energetsku razinu (antiparalelna orijentacija). Opisani proces apsorpcije zračenja naziva se magnetska rezonancija. Energija toga prijelaza ovisi o neposrednom kemijskom okruženju apsorbirajuće jezgre u molekuli, pa je to osnova primjene nuklearne magnetske rezonancije.
Posebno je važna magnetska rezonancija jezgri vodika (protona) i ugljikova izotopa 13C u organskim molekulama i biomolekulama. Zbog nedestruktivnosti i mogućnosti detekcije čak stotinjak različitih jezgri, nuklearna magnetska rezonancija se proširila iz fizike u kemiju, biokemiju, biologiju, medicinu i drugo, te je postala nezaobilaznom tehnikom za određivanje strukture tvari, ali i za proučavanja dinamike i svojstava molekula u kapljevitom i čvrstom stanju. Iznimno važno mjesto ima danas u medicinskoj dijagnostici (magnetska rezonancija). Nuklearna magnetska rezonancija se rabi i u primijenjenim istraživanjima, na primjer u poljoprivredi za utvrđivanje vlažnosti i sastava žitarica, praćenje štetnih tvari u tlu i drugo, u kemijskoj industriji za određivanje čistoće i sastava proizvoda reakcija, otapala, eksploziva, boja, u prehrambenoj industriji za kontrolu masnoća, praćenje procesa zamrzavanja, određivanje autentičnosti vina, maslinova ulja, za atestiranje mlijeka, čokolade i slično.[2]
Elektronska paramagnetska rezonancija[uredi | uredi kôd]
Elektronska paramagnetska rezonancija (kratica EPR) ili elektronska spinska rezonancija (kratica ESR) je prijelaz između spinskih stanja nesparenog elektrona u atomima, ionima i molekulama paramagnetskih tvari u magnetskom polju. Spinski je kvantni broj elektrona 1/2, pa elektron ima dva spinska stanja. Rezonanciju elektronskoga spina pokazuju samo nespareni elektroni, jer se pri sparivanju elektrona njihovi spinovi poništavaju. Spektrometrijom EPR-a prijelazi između spinskih stanja rezonantno se pobuđuju elektromagnetskim zračenjem u mikrovalnom području. Spektar apsorbiranoga zračenja (broj, položaj, širina i relativni intenzitet spektralnih linija te međusobni razmak) odražava stanje okoline u izravnoj blizini nesparenog elektrona. Zbog njegove velike reaktivnosti malo je tvari u stabilnom stanju koje se tom tehnikom mogu istraživati. Takve su tvari električni vodiči i poluvodiči, u kojima se opažaju slobodni elektroni ili elektroni uhvaćeni u stupice, kompleksi prijelaznih metala (posebno u nekim enzimima) i nereaktivni ili slabo reaktivni slobodni radikali. Stabilni slobodni radikali često se upotrebljavaju kao priljepci na makromolekulama ili kao sonde u većim molekulskim strukturama (biološkim membranama, organelama, lipoproteinima, polimernim materijalima), pa se iz spektra EPR-a slobodnih radikala dobivaju informacije o organizaciji tih struktura.[3]
Izvori[uredi | uredi kôd]
- ↑ rezonancija, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2016.
- ↑ nuklearna magnetska rezonancija (NMR), [2] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2016.
- ↑ elektronska paramagnetska rezonancija, [3] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2016.













