Bernoullijeva jednadžba


Bernoullijeva jednadžba (prema Danielu Bernoulliju) je osnovni zakon gibanja fluida. Proizlazi iz primjene zakona o očuvanju energije na strujanje fluida. Odatle se dobije da zbroj:
ima istu vrijednost posvuda u fluidu koji struji vodoravno, gdje je p tlak, ρ gustoća i v brzina fluida u nekoj točki, a h visina visina težišta poprečnog presjeka fluida u odnosu na neku vodoravnu ravninu. Prema tome, ondje gdje je brzina tekućine veća, tlak je manji, ondje gdje je brzina tekućine manja, tlak je veći. Na Bernoullijevoj jednadžbi osnivaju se mnoge inženjerske primjene, kao na primjer let zrakoplova: zrak struji uz gornju zakrivljenu plohu krila brže nego ispod krila, pa je tlak na donju plohu krila veći nego na gornju, što ima za posljedicu da na krila djeluje ukupna sila prema gore koja diže zrakoplov.[1]
Bernoullijeva jednadžba prikazuje odnos između brzine, tlaka i gustoće tekućine u kretanju. Ona kaže da je u slučaju stabilnog strujanja nestlačive idealne tekućine, bez trenja, ukupna energija tekućine jednaka duž svih prereza; porastom brzine tekućine pada njen hidrostatski tlak i obratno. Zbroj hidrostatskog tlaka i hidrodinamičkog tlaka u vodoravnom strujanju daje ukupan tlak koji je konstantan u svim prerezima cijevi. Drugim riječima, Bernoullijeva jednadžba predstavlja zakon očuvanja energije koji nam u slučaju stacionarnog strujanja tekućine govori da za vrijeme stacionarnog strujanja jedinica mase tekućine (njen diferencijalni dio) ima konstantnu energiju duž cijele strujne cijevi.
Energija tekućina[uredi | uredi kôd]


Tekućine mogu imati energiju u različitim oblicima.
Potencijalna energija tekućina[uredi | uredi kôd]
Tekućina mase m (kg), koja se nalazi na nekoj visini z (m), mjerenoj od neke vodoravne ravnine, ima potencijalnu energiju:
Naime s te visine tekućina se može spustiti i izvršiti rad kolika je njezina potencijalna energija. Visina z, na kojoj se tekućina nalazi, zove se geodetska visina. Ona se mjeri geodetskim instrumentom, totalnom stanicom ili teodolitom.
Tlačna energija tekućine[uredi | uredi kôd]
Tekućina ima energiju i zbog hidrostatskog tlaka p. Priključimo na izlaznu cijev posude, u kojoj se nalazi tekućina, jednu usku cijev. Tekućina će se u toj cijevi dignuti na visinu h, koja odgovara hidrostatskom tlaku, to jest:
a tlačna energija ove tekućine obujma V jest:
Visina na koju se tekućina podigne zbog hidrostatskog tlaka zove se manometarska visina.[2]
Kinetička energija tekućine[uredi | uredi kôd]
Zamislimo da imamo rezervoar u koji dotječe tekućina sa strane tako da uvijek stoji na istoj razini. Na dnu rezervoara nalazi se otvor kroz koji tekućina istječe. Tekućina mase m (kg) na nekoj visini h ima potencijalnu energiju m ∙ g ∙ h. Kad tekućina istječe kroz otvor na dnu rezervoara, potencijalna se energija tekućine pretvara u kinetičku energiju, pa mora biti:
gdje je v brzina istjecanja tekućine. Iz ovog izraza proizlazi da je visina tekućine, na koju bi se ona popela zbog kinetičke energije:
Ta visina, koja daje tekućini brzinu v, zove se visina brzine i ona je mjerilo za kinetičku energiju tekućine.
Objašnjenje Bernoullijeve jednadžbe[uredi | uredi kôd]
Da bi se objasnila Bernoullijeva jednadžba, na lijevu posudu se dodaje vodoravna staklena cijev koja se sužuje i na sebi ima uspravne staklene cijevčice. Začepimo li otvor na kraju cijevi desno i napunimo li posudu vodom do visine h, voda će po zakonu o spojenim posudama stajati svuda jednako visoko do visine h. Kad vodoravnu cijev desno otčepimo, voda će početi istjecati i ona neće u svim cjevčicama stajati jednako visoko, što znači da tlakovi u tekućini koja struji nisu na svim mjestima jednaki. Vidimo da je tlak na kraju cijevi desno jednak nuli, a odavde prema unutrašnjosti jednakomjerno raste, što pokazuje pravac koji spaja vrhove stupaca vode u okomitim cjevčicama. Znači da tlak pada ravnomjerno (proporcionalno) s duljinom cijevi. Pad tlaka je smanjenje tlaka na jedinici duljine cijevi. Prema tome zaključujemo da je strujanje tekućina kroz dugačke cijevi drugačije u pogledu tlaka, a i brzine, nego što to daje Torricellijev zakon istjecanja. Tlak koji tekućina ima u strujanju zove se hidrodinamički tlak.

Iz pokusa vidimo da tlak u vodoravnoj cijevi stalno opada, te da je hidrodinamički tlak na svakom mjestu manji od hidrostatskog tlaka koji bi postojao kad mi voda mirovala. Ako je cijev svuda istog presjeka, to po principu kontinuiteta brzina mora biti svuda ista. Ovo je moguće samo stoga što su čestice vode tjerane stalnim tlakom (to jest stalnom silom), jer bi inače trenje postepeno uništilo njihovu kinetičku energiju. Visina h1 stupca vode u strujanju predstavlja visinu otpora, to jest onaj tlak koji je potreban za svladavanje otpora duž cijevi. Visina h2 je visina brzine koja daje tekućini brzinu u strujanju. Odatle vidimo da se hidrostatski tlak h djelomično troši na svladavanje otpora, a preostali dio daje tekućini brzinu.
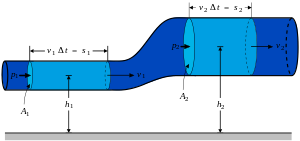
Da bismo ustanovili po kojem se zakonu vlada tlak kod tekućine u strujanju, uzet ćemo u razmatranje jednu nagnutu cijev kojoj se presjek prema kraju smanjuje. Budući da po zakonu kontinuiteta kroz svaki presjek mora proći u jedinici vremena ista količina tekućine, to će brzine u raznim presjecima biti različite. Tako će u presjeku I brzina biti v1, u presjeku II brzina v2, a u presjeku III brzina v3. Zanemarimo li trenje (idealna tekućina), u svakoj točki strujnog mlaza mora, po zakonu o održanju energije, ukupna energija ostati uvijek ista. Uzmimo da kroz svaki presjek u jedinici vremena prolazi m kilograma tekućine.
U položaju I energija tekućine sastoji se od 3 dijela:
- od potencijalne energije, koja iznosi m ∙ g ∙ z1, gdje se visina z1 mjeri od nivoa istjecanja,
- od tlačne energije p1 ∙ V,
- od kinetičke energije m ∙ v12 / 2.
Prema tome vrijedi, u položaju I:
u položaju II:
u položaju III:
Kako smo pretpostavili da nema trenja, to po zakonu o održanju energije mora biti:
odnosno općenito vrijedi:

To je Bernoullijev zakon strujanja, koji glasi: Zbroj tlačne, potencijalne i kinetičke energije pri stacionarnom strujanju idealne tekućine je konstantna veličina.
Podijelimo li gornju jednadžbu s V, dobivamo:
jer za gustoću tekućine vrijedi:
dobivamo:
a to je Bernoullijeva jednadžba koja se odnosi na jedinicu mase idealne tekućine. Svi članovi u ovom izrazu imaju jedinicu tlaka. Veličina ρ ∙ v2 / 2 zove se hidrodinamički tlak, jer njegova vrijednost ovisi o brzini tekućine.
Podijelimo li gornji izraz s ρ ∙ g dobijemo:
Ovo je oblik Bernoullijeve jednadžbe koji se odnosi na jedinicu težine idealne tekućine. Njeni članovi imaju dimenziju duljine. Naime p / ρ g = h i predstavlja manometarsku visinu, odnosno energiju jedinice težine tekućine. Naime, energija tekućine težine G jest:
Ako je G = 1, onda je energija p / ρ ∙ g. Član z je geodetska visina i predstavlja potencijalnu energiju težine tekućine. Naime, tekućina težine G ima na visini z energiju G ∙ z. Ako je G = 1, onda je potencijalna energija jednaka z. Član v2 / 2 ∙ g je visina brzine, te ima također dimenziju duljine, to jest brojčano daje kinetičku energiju jedinice težine tekućine. Naime, tekućina težine G, to jest mase m = G / g i brzine v ima kinetičku energiju G / g v2 / 2, a tekućina težine G = 1 ima kinetičku energiju v2 / 2 ∙ g.
Prema tome, možemo Bernoullijevu jednadžbu izraziti i ovako: Pri stacionarnom strujanju idealne tekućine je zbroj geodetske visine, manometarske visine i visine brzine u svakoj točki duž strujanja stalna veličina.
Označimo li ukupni tlak u tekućini koja struji s po, možemo napisati i ovako:
Protiče li tekućina kroz vodoravnu cijev, onda je z = 0, pa je:
Iz toga proizlazi da je zbroj hidrostatskog i hidrodinamičkog tlaka idealne tekućine na svim mjestima vodoravnog cjevovoda konstantan. Iz prethodnog izraza proizlazi također važan zaključak koji daje odnos između tlaka p i brzine v u svakom presjeku. Naime, po zakonu kontinuiteta proizlazi da je u većem presjeku neke cijevi brzina malena, a iz Bernoullijeve zakona strujanja izlazi da se u tom slučaju tlak p mora povećati kako bi ukupan tlak po ostao isti. Iz toga se vidi da je kod strujanja tekućine brzina u većem presjeku malena, a tlak velik, dok je u malom presjeku brzina velika, a tlak malen. Sniženje tlaka pare ili plinova kod prolaza kroz uske otvore zove se prigušivanje ili prigušenje. Bernoullijev zakon vrijedi i za plinove. Kod strujanja plinova razlikujemo aerodinamički i aerostatički tlak.
Osnovne i izvedene mjerne jedinice koje se koristi Bernoullijeva jednadžba[uredi | uredi kôd]
- ρ = Gustoća -
- S = presjek predstavlja površinu poprečnog presjeka ili Ploština - .
- p = statički tlak - (Pa)
- v = brzina - (m/s)
- m = masa tekućine - (kg)
- R = mehanički rad - (J)
- V = volumen mase tekućine -
Bernoullieva jednadžba koristi SI sustav jedinica.
- = geodetska visina odnosno visina težišta poprečnog presjeka u odnosu na neku vodoravnu ravninu u
- = pijezometarska ili tlačna visina odnosno visina pijezometarskog tlaka koju pokazuje visina stupca tekućine u pijezometarskoj cijevi u
- = brzinska visina u , a brzina predstavlja brzinu koju bi tijelo imalo kada bi bilo u slobodnom padu.
- Ukupan zbroj energija daje Bernoullijevu jednadžbu
Ulaskom u uži dio cijevi, presjeka i statičkog tlaka tekućina dobije veću brzinu . Masa tekućine m ima u širem dijelu cijevi kinetičku energiju:
- a kad uđe u uži dio kinetičku energiju:
Povećanje kinetičke energije posljedica je mehaničkog rada R koji je nastao radi razlike tlakova () pri gibanju mase m tekućine iz šireg dijela cijevi u uži na putu ΔS:
- R = () ΔS
- R= () V, gdje je V volumen mase tekućine.
Taj je rad jednak povećanju kinetičke energije:
- () V = -
Dijeljenjem gornje jednakosti s volumenom, znajući da je gustoća ρ = dobivamo Bernoullijevu jednadžbu:
- + = + = + = konst.
Izrazi , + i + prikazuju tlak koji je nastao zbog strujanja tekućine i zove se dinamički tlak.
Oblik Bernoullijeve jednadžbe za idealnu tekućinu[uredi | uredi kôd]
- Osnovne pretpostavke pod kojim vrijedi ova jednadžba su:
- tekućina je idealna - nestlačiva tekućina, linija energije je konstantna duž presjeka
- Stacionarno strujanje
- predstavlja hidrodinamički tlak ili ukupnu specifičnu energiju u .
Izvod Bernoullieve jednadžbe preko zakona održanja količine gibanja[uredi | uredi kôd]
- Bernoullijeva jednadžba je prvi puta izvedena 1738. godine primjenom zakona održanja količine gibanja.
Osnovne pretpostavke pod kojima vrijedi ovaj izvod su:
- fiktivna cijev ili proračun za konačni element neke cijevi,
- Stacionarno strujanje ili postupno promjenjivo strujanje.
Izvod Bernoullieve jednadžbe preko Eulerovog integrala[uredi | uredi kôd]
- Eulorove diferencijalne jednadžbe kretanja tekućine - implicitni oblik
... ... ...(1E)
... ... ...(2E)
... ... ...(3E)
- nema općeg rješenja jer imamo 4 nepoznanice. Rješenje je moguće samo ako definiramo pretpostavku koja će eliminirati nepoznanicu viška.
- Osnovna pretpostavka:
- imamo stacionarno strujanje
- matematičke transformacije - (1E) množimo s dx, (2E) množimo s dy, (3E) množimo s dz i sumiramo dobivene jednadžbe.
pa dobijemo jednadžbu:
možemo derivirati
dakle, sada imamo ovaj oblik jednadžbe
- ako imamo strujnu cijev u kojoj dijeluje samo gravitacija u normalnom koordinatnom sustavu. Možemo pojednostaviti ovako;
I konačno Eulerov integral koji predstavlja izvod bernoullieve jednadžbe:
Oblik Bernoullijeve jednadžbe za realnu tekućinu[uredi | uredi kôd]
- je dio specifične energije utrošen na svladavanje hidrodinamičkih otpora strujanju kapljevine. Izražava se u .
Coriolisov koeficijent[uredi | uredi kôd]
Ili koeficijent kinetičke energije . On pokazuje odnos stvarne kinetičke energije mase fluida koji protječe poprečnim presjekom u jedinici vremena i kinetičke energije određene iz uvjeta da su brzine u svim točkama presjeka jednake (srednja brzina). Koeficijent kinetičke energije je bezdimenzionalna jedinica.
- Koeficijent kinetičke energije najčešće ima sljedeće vrijednosti:
- kod strujanja u cijevima
- kod strujanja u otvorenim vodotocima
- vrijednost možemo računati ovom formulom:
- postavlja se uvjet da je
Praktična primjena Bernoullijeve jednadžbe[uredi | uredi kôd]
Na Bernoullijevoj jednadžbi osnivaju se mnoge inženjerske primjene, kao na primjer let zrakoplova: zrak struji uz gornju zakrivljenu plohu krila brže nego ispod krila, pa je tlak na donju plohu krila veći nego na gornju, što ima za posljedicu da na krila djeluje ukupna sila prema gore koja diže zrakoplov.
Primjer cijevi pod tlakom[uredi | uredi kôd]

znamo: .
- gubitak tlaka predstavlja razliku pijezometarskih visina u presjecima (1) i (2). Za slučaj da je cijev vodoravna vrijedi:
Primjer za otvoreni vodotok[uredi | uredi kôd]

znamo: ako je strujanje jednoliko
- atmosferski tlak djeluje na površini vodotoka
- u pijezometrima se voda podiže do razine vode u vodotoku
- linija vodnog lica je pijezometarska linija


Primjer za Venturijev vodomjer[uredi | uredi kôd]
gdje je hidrostatski tlak, dinamički tlak, a ukupni tlak, konstantan u cijelom vodoravnom cjevovodu bez obzira na presjek.
- Bernoullijev zakon ili Bernoullijeva jednadžba služi za proračun brzine, tlaka ili gubitaka kod tečenja tekućine kroz otvorene i zatvorene vodotoke za idealnu i realnu tekućinu. Pošto se radi o tekućinama ,tj. fluidima, Bernoullieva jednadžba služi kao temeljna postavka za objašnjavanje uzgona aeroprofila.
Venturijeva cijev[uredi | uredi kôd]
Venturijeva cijev (po talijanskom fizičaru Giovanniju Battisti Venturiju; 1746. – 1822.) je uređaj ili mjerni instrument za mjerenje brzine strujanja fluida (tekućina ili plin). Prema Bernoullijevoj jednadžbi, ukupni tlak u fluidu u gibanju to je manji što je brzina strujanja veća. Obrnuto, iz poznavanja razlike tlaka u mirnom fluidu i fluidu koji struji može se izračunati brzina strujanja, odnosno brzina tijela koji je to strujanje izazvao. Na tom se načelu temelji Venturijeva cijev. U širem dijelu posude fluid struji sporije nego u uskom dijelu pa je u širem dijelu tlak veći. Razlika tlakova p = p1 – p2 mjeri onda i brzinu strujanja:
Venturijeva cijev služi za određivanje brzine zrakoplova i mjerenja u zračnim tunelima.[3]
Rasplinjač[uredi | uredi kôd]
Rasplinjač (ponegdje karburator) je dio nekih Ottovih ili benzinskih motora, koji miješanjem goriva sa zrakom priprema određenu količinu gorive smjese i potom ju raspršuje u cilindar. Gorivo se iz spremnika dovodi u komoru s plovkom koji regulira dotok goriva, iz koje se kroz difuzor (Venturijeva cijev) raspršuje i miješa u određenom omjeru sa zrakom, te naposljetku usisava u motor gdje izgara. Najpovoljnije izgaranje gorive smjese odvija se pri omjeru goriva (benzina) i zraka 1 : 15. Rasplinjači su tako konstruirani da daju motoru smjesu bogatiju gorivom pri puštanju u pogon i pri punom opterećenju, a jeftinu (ekonomičnu) smjesu pri opterećenju od 60 do 70% snage. Rasplinjače imaju Ottovi motori s vanjskom pripremom gorive smjese. Za pogon putničkih automobila počeli su se sredinom 1990-ih primjenjivati i motori s izravnim ubrizgavanjem goriva u cilindar u koji je prethodno usisan zrak, to jest motor s unutarnjom pripremom gorive smjese.[4]
Rasplinjač je bio među prvim patentima Carla Benza, jer je on razvio motor s unutarnjim izgaranjem i njegove dijelove. Godine 1885. Wilhelm Maybach i Gottlieb Daimler razvili su rasplinjač za njihov motor, koji se temelji na načelu štrcanja mlaznica. Rasplinjači su bili uobičajeni dio benzinskih motora proizvedenih u većem dijelu SAD-a do kasnih 1980-ih, kada je ubrizgavanje goriva (eng. fuel injection] postalo sve učestalije. U ostatku svijeta, određeni automobili marke rabe rasplinjač, kao primjerice Lada, koja ga je rabila do 2006. Većina motorkotača i dalje rabi rasplinjač zbog nižih troškova, ali od 2005. mnogi novi modeli uvode ubrizgavanje goriva.

Bunsenova sisaljka[uredi | uredi kôd]
Bunsenova sisaljka sastoji se od jedne zatvorene posude u koju ulazi cijev, na kraju sužena. Na tu cijev nadovezuje se druga s proširenim otvorom. Posuda je spojena s jednom cijevi iz koje želimo, na primjer, sisati zrak ili neku tekućinu. Takva se sisaljka može priključiti na vodovod. Kad kroz cijev struji voda, na mjestu suženja brzina toliko naraste da tlak padne ispod atmosferskog tlaka. Zbog toga se kroz priključnu cijev siše zrak ili tekućina s vodom iz sisaljke.
Bunsenov plamenik[uredi | uredi kôd]
Bunsenov plamenik sastoji se od jedne šire cijevi koja po strani ima otvore. U toj cijevi nalazi se manja cijev koja se na kraju sužuje, a zove se sapnica. Kroz sapnicu izlazi velikom brzinom plin, te kroz otvore siše zrak, potreban za njegovo potpuno izgaranje.
Injektor[uredi | uredi kôd]
Injektor (prema lat. iniectus, particip prošli od inicere: ubaciti), u strojarstvu, je uređaj za napajanje parnih kotlova napojnom vodom. Djeluje na istome načelu kao i ejektor, slične je konstrukcije i nema pokretnih dijelova. Stoga je njegov rad pouzdan, ali se zbog slabe energetske iskoristivosti primjenjuje za napajanje kotlova nižih radnih tlakova ili kao pomoćno sredstvo za napajanje.
U širem smislu, naziv injektor (brizgaljka) veže se u tehnici uz uređaje ili dijelove uređaja kojima se, primjerice, injektira (ubrizgava) gorivo u Ottov motor (benzinski motor) s izravnim ubrizgavanjem ili u Dieselov motor, ili pak beton ili cementna smjesa u šupljine tla ili građevine (injektiranje) i slično.[5]
Ejektor[uredi | uredi kôd]
Ejektor (prema lat. eiectus, particip prošli od eicere: izbacivati) je naprava za crpenje i usisavanje pare, plina ili tekućine; služi za isisavanje zraka iz kondenzatora parnih postrojenja, za provjetravanje rovova u rudnicima i slično. Djeluje na načelu smanjenja tlaka u suženom presjeku cijevi (Venturijeva cijev) kroz koju struji mlaz nekog fluida, najčešće pare, vode ili zraka. Na primjer kod parnog ejektora, para se dovodi u ejektor preko prigušnoga ventila kojim se regulira tlak pare, a time i brzina istjecanja pare iz sapnice. Sapnica je smještena u komori za miješanje, gdje zbog strujanja pare nastaje podtlak. Mješavina pare i medija koji se isisava dalje struji kroz suženu cijev i difuzor u hladnjak (kondenzator) ili se izbacuje u atmosferu. Za postizanje većeg podtlaka upotrebljavaju se dvostupanjski i višestupanjski ejektori. Na isti način rade i injektori, koji služe za napajanje parnih kotlova nižih radnih tlakova i kapaciteta.[6]
Sis broda[uredi | uredi kôd]
Sis je međusobno privlačenje brodova koji plove u istom smjeru. Kad dva broda plove na maloj udaljenosti u istom smjeru, onda je brzina strujanja vode između brodova velika, a tlak malen. Zbog toga je tlak na njihove bokove s vanjske strane veći nego s unutarnje. Brodovi se zbog toga približavaju i može doći do sudara. Takav je slučaj naročito opasan kad je jedan malen, a drugi velik.
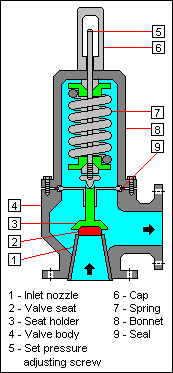
Ventil za ograničavanje tlaka ili redukcijski ventil[uredi | uredi kôd]
Ventil za ograničavanje tlaka osigurava da tlak u sustavu (npr. hidraulički pogon) ne prijeđe maksimalno dopuštenu vrijednost. Koriste se kao sigurnosni ventili (za zaštitu od prekomjernog tlaka), kao kočni ventili (za zaštitu od tlačnih udara koji nastaju npr. prilikom zatvaranja razvodnika) ili kao ventili za protudržanje. Potrebni su i prisutni u svim hidrauličkim sustavima, tipično se postavljaju na izlazu hidrauličke pumpe, za zaštitu pumpe i sustava od prekomjernog tlaka.[7]
Ventil za ograničavanje tlaka u normalnom je položaju zatvoren. Na ventilu se skraćivanjem ili produžavanjem opruge namjesti željeni maksimalni tlak pri kojem će pritisak na pladanj ventila svladati silu u opruzi, gurnuti pladanj i na taj način otvoriti ventil. Tlak otvaranja veći je od tlaka zatvaranja ventila za 10 - 15% (histereza). U ventile za ograničenje tlaka često se ugrađuju prigušni klipovi ili prigušnice za smanjenje brzine zatvaranja (brzo otvaranje i usporeno zatvaranje). Time se sprječavaju štete od tlačnog udara kakvi se javljaju npr. ako se zatvaranjem ventila trenutačno obustavi protok prema nekom potrošaču.
Ventil za ograničavanje tlaka izvodi se kao direktni do nazivnog tlaka NP 10, dok se za veće tlakove (zbog povećanih sila) koriste indirektno upravljani ventili.
Izvori[uredi | uredi kôd]
- ↑ Bernoullijeva jednadžba. Hrvatska enciklopedija. Leksikografski zavod Miroslav Krleža. 2015.
- ↑ Velimir Kruz: "Tehnička fizika za tehničke škole", "Školska knjiga" Zagreb, 1969.
- ↑ Venturijeva cijev. Hrvatska enciklopedija. Leksikografski zavod Miroslav Krleža. 2016.
- ↑ rasplinjač. Hrvatska enciklopedija. Leksikografski zavod Miroslav Krleža. 2016.
- ↑ injektor. Hrvatska enciklopedija. Leksikografski zavod Miroslav Krleža. 2016.
- ↑ ejektor. Hrvatska enciklopedija. Leksikografski zavod Miroslav Krleža. 2016.
- ↑ [1] Arhivirana inačica izvorne stranice od 18. srpnja 2013. (Wayback Machine) "Pneumatika i hidraulika" Radoslav Korbar, Veleučilište u Karlovcu, www.vuka.hr, 2007.











































































